Следующая страница: Заключение
Предыдущая страница: Глава 5.
``Изменение орбитальной симметрии локализованного
3d1 электрона иона
V4+ при переходе
металл - изолятор в VO2''
Вернуться к содержанию диссертации
Параграфы:
Глава 6. Магнитные свойства
Ca(Mg)VnO2n+1
Механизм формирования щели в спектре спиновых возбуждений в низкоразмерных
спин-1/2 системах, описывающихся с помощью модели Гейзенберга
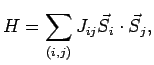 |
(6.1) |
в последние несколько лет является объектом неослабного
научного исследования. Один из путей описания физической природы двумерных
гейзенберговских антиферромагнетиков, имеющих (квази-)квадратную решетку,
является изучение проблемы о том, каким образом магнитные свойства этих
объектов, имеющих лестничную структуру, зависят от числа ног лестниц и от
взаимодействия между ними. Изучение лестничных структур интересно и само по
себе в теоретическом плане. Исходя из теоретического описания, лестницы с
нечетным числом ног и антиферромагнитным взаимодействием между лестничными
ногами и перекладинами не должны иметь энергетической щели в спектре
спиновых возбуждений при переходе от основного синглетного спинового
состояния S=0 в ближайшее по энергии триплетное
возбужденное состояние
S=1. В то же время лестницы с четным числом ног
должны иметь эту спиновую
щель при любом конечном антиферромагнитном взаимодействии между
перекладинами [252]. Для лестниц с четным числом ног и с
отношением обменных интегралов
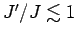 взаимодействий вдоль
перекладин J' и вдоль ног J
величина спиновой цели уменьшается
экспоненциально с увеличением числа ног [253]. Спиновая щель
существует и в случае, когда взаимодействие J -
антиферромагнитно, а
J' - ферромагнитно, хотя закон изменения величины щели
иной, чем в
предыдущем случае: происходит переход второго рода между двумя основными
состояниями со спиновой щелью в тот момент, когда эта щель схлапывается при
переходе через 0 с изменением знака (от анти- к ферромагнитному
взаимодействию) величины J' [254]. Принимая во внимание всю
сложность теоретических предсказаний, при изучении какой-либо реальной
лестничной системы априори нельзя предсказать, будет
ли она иметь энергетическую щель в спектре спиновых возбуждений; и
требуется детальное изучение сверхобменных взаимодействий для предсказания
или корректного описания магнонного спектра.
взаимодействий вдоль
перекладин J' и вдоль ног J
величина спиновой цели уменьшается
экспоненциально с увеличением числа ног [253]. Спиновая щель
существует и в случае, когда взаимодействие J -
антиферромагнитно, а
J' - ферромагнитно, хотя закон изменения величины щели
иной, чем в
предыдущем случае: происходит переход второго рода между двумя основными
состояниями со спиновой щелью в тот момент, когда эта щель схлапывается при
переходе через 0 с изменением знака (от анти- к ферромагнитному
взаимодействию) величины J' [254]. Принимая во внимание всю
сложность теоретических предсказаний, при изучении какой-либо реальной
лестничной системы априори нельзя предсказать, будет
ли она иметь энергетическую щель в спектре спиновых возбуждений; и
требуется детальное изучение сверхобменных взаимодействий для предсказания
или корректного описания магнонного спектра.
Рис. 6.1:
Экспериментальный спектр магнонного возбуждения в
CaV4O9.
Рисунок воспроизведен из работы [255].
|
|
Примером систем со спином S=1/2, имеющих лестничную
структуру, являются семейство слоистых оксидов
Ca(Mg)VnO2n+1
четырехвалентного ванадия. Особый интерес в ряду этих соединений вызывает
CaV4O9
- первый пример квази-двумерной системы с щелью в спектре спиновых возбуждений
(рис. 6.1), возникающей вследствие фрустрированного
состояния резонансной валентной связи на плакетках (квадратах) ванадия
[256]. Интересны также свойства и других
членов данного
семейства, например, существование сложного спинового упорядочения в
CaV3O7
[8], а также существенное отличие величин
щели в спектре спиновых возбуждений оксидов
CaV2O5
и MgV2O5
[257, 258]. Необходимо отметить, что несмотря на
большое
количество как экспериментальных, так и теоретических работ, магнитные
свойства этих материалов до сих пор не получили полного объяснения. В
противоположность слоистым оксидным соединениям меди, где расположенная на
Cu  орбитали электронная дырка приводит к сильному
180o антифферомагнитному и слабому
90o ферромагнитному
металл-кислород-металл взаимодействиям, природа обменных взаимодействий в
случае
Ca(Mg)VnO2n+1
имеет более сложный характер. В главе
представлены результаты исследования электронной структуры и расчетов
параметров межузельного обменного взаимодействия в
CaV2O5,
MgV2O5,
CaV3O7 и
CaV4O9
неэмпирическим методом LDA+U.
орбитали электронная дырка приводит к сильному
180o антифферомагнитному и слабому
90o ферромагнитному
металл-кислород-металл взаимодействиям, природа обменных взаимодействий в
случае
Ca(Mg)VnO2n+1
имеет более сложный характер. В главе
представлены результаты исследования электронной структуры и расчетов
параметров межузельного обменного взаимодействия в
CaV2O5,
MgV2O5,
CaV3O7 и
CaV4O9
неэмпирическим методом LDA+U.
Кристаллическая структура
Основным элементом кристаллических структур исследуемых соединений ряда
Ca(Mg)VnO2n+1
являются кислородные пирамиды с ионами ванадия,
расположенными вблизи их геометрических центров.
Соединяясь друг с другом, они образуют так называемые ванадиевые плакетки
или квадраты, которые в
CaV2O5 и
MgV2O5
составляют двуногие
лестницы, а в случае
CaV3O7
образуют зигзагообразные цепочки. В
структуре CaV4O9
атомы ванадия, находяшиеся по одну сторону от
кислородной плоскости, формируют уже метаплакетки (термин предложен
Пикеттом с целью отличить их от плакеток, образованных ионами V,
находящимися на кратчайшем расстоянии друг от друга [259]).
Рис. 6.2:
Кристаллическая структура
CaV2O5.
Сферы
малого радиуса обозначают кислороды, большого - ионы ванадия. Ионы кальция
на рисунке не показаны. Их положение проектируется на квадраты, свободные
от атомов ванадия (см. правый рисунок). Слева - вид элементарной ячейки
сбоку, справа - вид сверху на V-O плоскость. На правом рисунке атомы V,
имеющие одинаковую координату по вертикальной оси, обозначены одинаковым
цветом: темно-серые расположены над плоскостью, светло-серые - под
плоскостью. Показан элемент лестницы, у которой ноги изображены сплошными
линиями, перекладины - пунктирными.
|
|
Кристаллическая структура
CaV2O5 -
примитивная орторомбическая, пространственная группа Pmmn [260]. Как предствлено на
рис. 6.2, структура образована сцеплением пирамид
VO5,
имеющих атомы вершинных кислородов в направлении оси c. Атомы V,
имеющие одинаковую координату z и чьи кислородные пирамиды соединены
вершинами
пирамид и вершинные атомы O в которых направлены в одинаковую сторону от
плоскости, образуют двуногую лестницу с ногами вдоль кристаллографического
направления b и перекладинами вдоль a. Атомы Ca расположены между
плоскостями, и каждый атом Ca имеет в ближайшем окружении 8 атомов
кислорода.
Рис. 6.3:
Кристаллическая структура
MgV2O5.
Сферы малого
радиуса обозначают кислороды, большого - ионы ванадия. Ионы магния на рисунке
не представлены.
|
|
Рис. 6.4:
Две VO5 пирамиды, соединенные вершинами.
Величины различных углов, отмеченных на рисунке, приведены в
таб. 6.1
|
|
Таб. 6.1:
Структурные данные для соединений
CaV2O5 и
MgV2O5.
Постоянные решетки в : a - вдоль перекладины лестницы,
b - вдоль ноги лестницы и c - в вертикальном направлении
(внимание:
эти соответствия направлениям отличаются от тех, которые приняты для групп
Pmmn и Cmcm). Расстояния в между ближайшими атомами V,
принадлежащими разным лестницам, вдоль ноги, вдоль перекладины и диагонали
между вершинами перекладин обозначены соответственно как
dnn,
dleg, drung и
ddiag. Обозначение углов
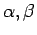 и
и
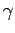 иллюстрированы на рис. 6.4,
а величины приведены в градусах.
иллюстрированы на рис. 6.4,
а величины приведены в градусах.
| Характеристика |
CaV2O5 |
MgV2O5 |
| a, b, c |
11.35, 3.60, 4.89 |
11.02, 3.69, 9.97 |
|
dnn,
drung,
dleg(=b),
ddiag |
3.03, 3.49, 3.60,
5.02 |
2.98, 3.57, 3.69, 5.00 |
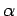 , , 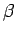 , , 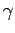 |
132.91,
102.94, 135.29 |
117.57, 109.23, 141.15 |
Кристаллическая структура
MgV2O5
- базоцентрированная орторомбическая, пространственная группа Cmcm [258]. Отличие от
CaV2O5
заключается в том, что ноги лестниц направлены вдоль a, а
также в том, что лестницы, находящиеся друг над другом в направлении b,
сдвинуты относительно друг друга на пол-периода
(рис. 6.3).
Каждый атом Mg окружен шестью атомами кислорода. Но наиболее существенным
элементом разницы кристаллических структур
CaV2O5
и MgV2O5
является отличие в длинах связи V-V и углах O-V-O. На рис.
6.4 представлены обозначения, использующиеся в
таб. 6.1 с детальными структурными данными для двух
рассмотренных соединений.
Рис. 6.5:
Кристаллическая структура
CaV3O7.
Сферы
малого радиуса обозначают кислороды, среднего - ионы ванадия, большого -
кальция. Слева - вид сбоку, справа - вид сверху на V-O плоскость (атомы
кальция не показаны). На правом рисунке атомы V, имеющие одинаковую
координату по вертикальной оси, обозначены одинаковым цветом: темно-серые
расположены над плоскостью, светло-серые - под плоскостью.
|
|
Кристаллическая структура
CaV3O7
- орторомбическая, пространственная группа Pnam, параметры решетки
a=10.459, b=5.295, c=10.382 ангстрем [261, 260]. Слоистая структура состоит из
наклоненных пирамид VO5,
соединенных гранями. Каждые две соседние
пирамиды имеют вершины, направленные в разные стороны. Атом ванадия
расположен внутри пирамиды: расстояние между ним и кислородной плоскостью в
основании пирамиды составляет 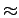 30% расстояния от вершинного
кислорода до этой плоскости. В плоскости V-O есть вакансии. Если
представить идеализированную квадратную решетку атомов ванадия, в которой V
образует шахматную доску, то вакансии появляются на шахматной доске в
местах остановки коня. Атомы кальция расположены между слоями вместо
отсутствующих пирамид (рис. 6.5).
30% расстояния от вершинного
кислорода до этой плоскости. В плоскости V-O есть вакансии. Если
представить идеализированную квадратную решетку атомов ванадия, в которой V
образует шахматную доску, то вакансии появляются на шахматной доске в
местах остановки коня. Атомы кальция расположены между слоями вместо
отсутствующих пирамид (рис. 6.5).
Рис. 6.6:
Слева - кристаллическая структура
CaV4O9.
Левый рисунок воспроизведен из работы [259]. Справа - вид
сверху на V-O плоскость. Атомы кислорода обозначены малыми шарами, атомы
ванадия - большими. Атомы ванадия, лежащие над плоскостью, обозначены
более темным цветом, чем находящиеся под плоскостью. Тонкими пунктирными
линиями обозначены плакетка, жирными пунктирными линиями - метаплакетка.
|
|
Кристаллическая структура
CaV4O9
- простая тетрагональная, пространственная группа P4/n,
параметры решетки a=8.333, c=5.008 ангстрем [262, 260]. Если вновь представить себе, что атомы
ванадия образуют шахматную доску, то вакансии по ванадиевой подрешетке
образуются движением правоходящего коня. Иначе картину распределения
вакансий можно получить, идя вдоль одного из направлений атомов ванадия,
удаляя каждый четвертый атом. Над (под) ванадиевыми вакасиями располагаются
атомы кальция. Пирамиды VO5,
как и для ранее рассмотренных соединений,
наклонены, атом ванадия располагается внутри пирамид
(рис. 6.6).
Электронная структура и обменные взаимодействия в CaV3O7
Изложение результатов начнем с соединения
CaV3O7
- единственного из
рассматриваемой серии, для которого наблюдается дальний магнитный порядок,
представленный на рис. 6.7.
Рис. 6.7:
Экспериментальная [8] магнитная
структура
CaV3O7,
спроектированная на идеализированную плоскость V-O.
Белые и черные круги обозначают ионы V с различной проекцией спина.
Кислородные атомы (на рисунке не показаны) располагаются в углах квадратов.
Ионы V, объединенные в светло-серые и серые плакетки, центрированные вокруг
ванадиевых вакансий, имеют (почти) одинаковые координаты по оси a. Также
показаны кристаллографические оси b и c и локальные оси координат
x и y.
|
|
Радиусы атомных сфер были выбраны 2.04 и 2.01 а.е. для двух типов V (атом V
типа 1 находится в бесконечной цепочке вдоль оси b; атом V типа 2
находится в трехзвенной цепочке вдоль оси c;
см. рис. 6.7), 2.15, 2.05, 1.61, 1.59 а.е. для
четырех типов кислорода,
3.32 а.е. для кальция, валентными орбиталями считались
4s, 4p, 3d для
V и Ca, 2s, 2p, 3d для О. Пять типов пустых сфер (27 штук на
формульную единицу) были введены в элементарную ячейку для заполнения
объема. При расчете реальной магнитной конфигурации элементарная ячейка
содержала две формульных единицы.
Рис. 6.8:
Полная и парциальные плотности состояний
CaV3O7,
полученные в LSDA расчете.
|
|
Рис. 6.9:
Вычисленное угловое распределение зарядовой плотности
d орбиталей ионов V4+
в плоскости bc в
CaV3O7.
Сферы малого радиуса обозначают кислороды.
|
|
Плотности состояний, полученные в самосогласованном LSDA расчете,
представлены на рис. 6.8. Расчеты предсказывают
полупроводниковый характер энергетического спектра
CaV3O7
с величиной щели в 0.3 эВ. Анализ матрицы заселенности V 3d оболочки совместно с
видом углового распределения V 3d спиновой плотности
(рис. 6.9) показывает, что единственный электрон
иона V4+
заселяет орбиталь типа xy в локальной системе координат, имеющую
минимальное перекрытие с O 2p орбиталями. Этот результат явился
неожиданным, поскольку ранее [8, 9] предполагалось,
что электрон занимает вырожденную
3dyz-3dzx
орбиталь. С целью ответить на вопрос о причинах
заполнения именно xy
орбитали были проведены модельные расчеты кластера
VO5, где в рамках
параметризации Слэтера-Костера [263] были использованы следующие
параметры:
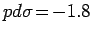 ,
,
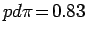 ,
,
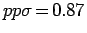 ,
,
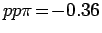 и
и
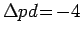 эВ. Установлено, что при смещении
иона V от основания пирамиды, не превышающем 10% ее высоты, наинизшим по
энергии является уровень, образованный состояниями yz и zx.
эВ. Установлено, что при смещении
иона V от основания пирамиды, не превышающем 10% ее высоты, наинизшим по
энергии является уровень, образованный состояниями yz и zx.
Однако более сильное смещение приводит к понижению уровня xy, и при
экспериментально наблюдаемых 30% это состояние становится ниже по энергии,
чем все остальные d-уровни. Данное расщепление настолько сильно,
что даже
при расчете электронной структуры этих соединений в рамках обычного
приближения спиновой плотности xy-зона отделена от других
V3d-зон относительно малой энергетической щелью
(рис.6.8).
Рис. 6.10:
Схема взаимодействия ионов
V4+ с
электроном, локализованном на орбитали
3dxy типа. Расстояния между
ионами V приведены в ангстремах. Ионы V, находящиеся в светло-серых и серых
плакетках, центрированных вокруг ванадиевых вакансий, имеют разные
координаты по оси a.
|
|
Каковы же могут быть взаимодействия между атомами V, если принять во
внимание орбитальную картину (рис. 6.9),
полученную в
расчете? На первый взгляд, должно быть сильное 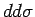 антиферромагнитное взаимодействие между ионами V из ближайших плакеток, в
то время как
антиферромагнитное взаимодействие между ионами V из ближайших плакеток, в
то время как 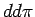 связь ионов V внутри плакетки ожидается значительно
слабее (рис. 6.10). Однако нельзя
пренебрегать влиянием
двух геометрических факторов. Действительно, расстояние между ближайшими
атомами V, принадлежащими разным плакеткам, меньше, чем в одной и той же
плакетке (2.98 и 3.00 ангстрем против 3.53 ангстрем). С другой стороны, ионы V,
принадлежащие разным плакеткам, имеют существенно разную координату по оси
a, что ослабляет прямое dd перекрытие. Поэтому для того чтобы
исследовать взаимодействия между атомами V, необходим расчет параметров
обменного взаимодействия с учетом реальной кристаллической структуры
CaV3O7.
связь ионов V внутри плакетки ожидается значительно
слабее (рис. 6.10). Однако нельзя
пренебрегать влиянием
двух геометрических факторов. Действительно, расстояние между ближайшими
атомами V, принадлежащими разным плакеткам, меньше, чем в одной и той же
плакетке (2.98 и 3.00 ангстрем против 3.53 ангстрем). С другой стороны, ионы V,
принадлежащие разным плакеткам, имеют существенно разную координату по оси
a, что ослабляет прямое dd перекрытие. Поэтому для того чтобы
исследовать взаимодействия между атомами V, необходим расчет параметров
обменного взаимодействия с учетом реальной кристаллической структуры
CaV3O7.
Рис. 6.11:
Парциальные плотности состояний двух типов V в соединении
CaV3O7,
полученные в LDA+U расчете. Вертикальной
штриховой линией обозначен уровень Ферми.
|
|
Расчет электронной структуры
CaV3O7
в приближении LDA+U был выполнен
с вычисленными величинами параметра одноузельного кулоновского взаимодействия
U=3.6 и параметра Стонера J=0.88 эВ.
Парциальные плотности
состояний атомов V приведены на рис. 6.11.
Разберем подробнее вопрос об орбитали, заселяемой электроном, скажем, на
атоме V первого типа (из бесконечной цепочки вдоль оси b). Один из таких
атомов находится в позиции (0.1890, 0.0205, -.1107)
в единицах
постоянной решетки. Матрица заселенности d орбитали (для простоты
изложения - спиновая матрица, то есть заселенность со спином вверх минус
заселенность со спином вниз), полученная в самосогласованном LDA+U расчете,
в кристаллографической системе координат такова:
Соответствие орбиталей диагональным элементам этой матрицы следующее: xy,
yz,
3z2-r2,
zx,
x2-y2.
Как видно по величине недиагональных
элементов представленной матрицы заселенности, в кристаллографической
системе координат заполненной будет орбиталь, являющаяся линейной
комбинацией xy,
3z2-r2
и
x2-y2
орбиталей. Перейдем в локальную
систему координат для этого атома V. Он находится в окружении пяти атомов
кислорода (первая колонка) в позициях (следующие 3 колонки) на расстоянии
(последняя колонка; а.е.):
Если локальную ось z направить на кислород 1, находящийся на ближайшем от
атома V расстоянии 3.011 а.е., а локальные оси x и y так,
чтобы они
смотрели на два из оставшихся четырех кислородов (минимизируя отклонения от
них с целью сохранения прямоугольности базиса), то углы Эйлера для перехода
в локальную систему координат будут
(-0.0835, -0.5109, 0.2561) в единицах
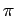 , а матрица заселенности в этой локальной системе координат будет
выглядеть как:
, а матрица заселенности в этой локальной системе координат будет
выглядеть как:
 |
(6.2) |
Как это видно из представленной матрицы, в локальной системе
координат заполненной является xy орбиталь (как это и отмечалось в тексте
главы ранее). Вместе с тем, наличие хоть и малых недиагональных элементов
матрицы заселенности вносит существенный вклад в обменное взаимодействие
между атомами V.
Одним из возможных путей установить природу
магнитных взаимодействий в соединениях рассматриваемого ряда
Ca(Mg)VnO2n+1
являются прямые расчеты параметров межузельного
обменного взаимодействия (Jij) из
``первых принципов''. В этих целях
была использована формула расчета Jij,
обменного интеграла модели
Гейзенберга (6.1), выведенная в работе [264] с помощью
метода функции Грина как вторая производная полной энергии основного
состояния системы по углу между направлениями магнитных моментов атомов
металла, находящихся в двух различных магнитных подрешетках:
 |
(6.3) |
где Nj - число ближайших соседей типа
j, и зависящий от
спина потенциал I записывается в виде разности матриц LDA+U потенциала:
 |
(6.4) |
а эффективная межрешеточная восприимчивость 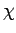 определяется в терминах
собственных функций
определяется в терминах
собственных функций 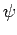 и собственных значений
и собственных значений 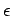 гамильтониана
метода LDA+U:
гамильтониана
метода LDA+U:
 |
(6.5) |
Здесь m - магнитное квантовое число:
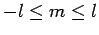 (l=2 для d функций и
l=3 для f функций), индекс n пробегает по
всем зонам, k - по всем точкам полной зоны Бриллюэна,
а функция
(l=2 для d функций и
l=3 для f функций), индекс n пробегает по
всем зонам, k - по всем точкам полной зоны Бриллюэна,
а функция
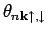 равна 1, если
соответствующая
равна 1, если
соответствующая
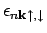 лежит не выше уровня
Ферми, и равна 0 в противоположном случае.
лежит не выше уровня
Ферми, и равна 0 в противоположном случае.
Параметр межузельного обменного взаимодействия
Jij имеет как величину,
так и знак. Для его определения необходимо провести спин-поляризованный
расчет и вычислить Jij в соответствии с
формулами (6.3) -
(6.5) между двумя подрешетками d атомов.
Если параметр
обменного взаимодействия будет иметь отрицательный знак, это означает, что
магнитное упорядочение, использовавшееся в расчете, было правильным. Если
знак параметра окажется положительным, то магнитная конфигурация в
спин-поляризованном расчете была задана неверно, и необходимо провести
новый расчет со спиновым упорядочением в соответствии со знаками
Jij.
Таким образом возможно предсказать магнитный порядок между d
(или f)
атомами в соединении, изначально не зная этого порядка из эксперимента.
Вычисление знака и величины обменного параметра дает альтернативный способ
предсказания спинового магнитного упорядочения в соединении в дополнение к
широко использующемуся способу сравнения полных энергий различных спиновых
конфигураций (см., например, главу 3).
Как будет показано ниже для соединений
Ca(Mg)V2O5 и CaV4O9,
возможно предсказание и
фрустрированных в магнитном отношении систем и вычисление обменных
взаимодействий в них.
LDA+U метод является аналогом метода Хартри-Фока для вырожденной модели
Хаббарда в приближении среднего поля. В то время как в случае многих
орбиталей приближение Хартри-Фока дает хорошие оценки полной энергии, то
для невырожденной модели Хаббарда приближение среднего поля недооценивает
разность энергий триплетного и синглетного состояния (и, соответственно,
величину эффективного обменного взаимодействия
Jij) в 2 раза для
двухчастичной задачи:
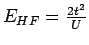 и
и
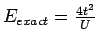 ,
где
,
где 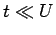 - интеграл межузельного перекрытия. Для рассматриваемых
соединений
Ca(Mg)VnO2n+1
имеется два типа вкладов в обменое
взаимодействие. Один из них происходит от взаимодействия орбиталей
xy-xy
на двух различных узлах. Поскольку только эти орбитали полузаполнены (с
учетом спина), xy-xy взаимодействие должно корректно
описываться
невырожденной моделью Хаббарда. Его величина должна быть умножена на
коэффициент 2 для приведения в соответствие результата в приближении
Хартри-Фока результату в невырожденной модели Хаббарда. Другой тип вклада
происходит из-за перескоков на все другие d орбитали и, поскольку
приближение среднего поля значительно лучше для многоорбитальной модели,
эти вклады не должны перенормироваться. Теперь становится ясным, что
наличие недиагональных элементов в матрице заселенности
(6.2),
описывающих перескоки с xy орбитали на все остальные d орбитали,
может
существенно изменить величину и даже знак параметра обменного
взаимодействия.
- интеграл межузельного перекрытия. Для рассматриваемых
соединений
Ca(Mg)VnO2n+1
имеется два типа вкладов в обменое
взаимодействие. Один из них происходит от взаимодействия орбиталей
xy-xy
на двух различных узлах. Поскольку только эти орбитали полузаполнены (с
учетом спина), xy-xy взаимодействие должно корректно
описываться
невырожденной моделью Хаббарда. Его величина должна быть умножена на
коэффициент 2 для приведения в соответствие результата в приближении
Хартри-Фока результату в невырожденной модели Хаббарда. Другой тип вклада
происходит из-за перескоков на все другие d орбитали и, поскольку
приближение среднего поля значительно лучше для многоорбитальной модели,
эти вклады не должны перенормироваться. Теперь становится ясным, что
наличие недиагональных элементов в матрице заселенности
(6.2),
описывающих перескоки с xy орбитали на все остальные d орбитали,
может
существенно изменить величину и даже знак параметра обменного
взаимодействия.
Обменное взаимодействие Jij в
CaV3O7
было рассчитано для пяти типов пар атомов V:
J1 и J2 -
между ближайшими соседями вдоль кристаллографических осей b и c
(атомы V в этих парах имеют существенно
разную координату по оси a); J3 -
взаимодействие в плакетке (атомы V
в этой паре имеют приблизительно одинаковую координату по оси a);
J4
- со вторым соседом по оси b (атомы V в этой паре имеют одинаковую
координату по оси a); J5 - с соседом
по оси c, находящимся через
вакансию по ванадиевой подрешетке (атомы V в этой паре имеют одинаковую
координату по оси a). Схема этих взаимодействий представлена на
рис. 6.12. Результаты расчета обменных
взаимодействий приведены в таб. 6.2.
Рис. 6.12:
Обозначения (использующиеся в таб. 6.2)
рассчитанных параметров обменного взаимодействия в
CaV3O7.
См. также рис. 6.5.
|
|
Таб. 6.2:
Рассчитанные параметры межузельного обменного взаимодействия (К) в
CaV3O7:
вклад от взаимодействия xy-xy
орбиталей (левая колонка цифр), вклад от взаимодействия остальных орбиталей
(средняя колонка) и суммарное обменное взаимодействие (правая колонка):
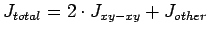 . Положительные величины
соответствуют антиферромагнитному взаимодействию, отрицательные -
ферромагнитному.
. Положительные величины
соответствуют антиферромагнитному взаимодействию, отрицательные -
ферромагнитному.
| |
xy-xy |
other |
total |
| J1 |
69 |
-92 |
46 |
| J2 |
34 |
-82 |
-14 |
| J3 |
37 |
1 |
75 |
| J4 |
9 |
0 |
18 |
| J5 |
3 |
-1 |
5 |
Как и ожидалось, наиболее значительными являются вклады в обменное
взаимодействие ближайших соседей
J1 и J2,
причем эти вклады имеют
разный знак от xy-xy орбиталей и остальных орбиталей.
В результате
абсолютное значение взаимодействий
J1 и J2
оказывается не так уж
большим по сравнению с J3. Вместе с тем для
взаимодействия J2 между
ближайшими соседями вдоль кристаллографической оси c вклад от остальных
орбиталей по абсолютному значению превысил удвоенный вклад от
xy-xy
орбиталей, что привело к ферромагнитному обмену
J2. Причиной различия
знаков J1 и J2
можно назвать разные наклоны соседних пирамид
VO5. Hаиболее сильным по
абсолютной величине является взаимодействие
между атомами V, находящимися по одну сторону от кислородной плоскости в
плакетке - J3.
Из всех рассматриваемых соединений только
CaV3O7
имеет магнитную
структуру с дальним порядком, которая однако не получила
удовлетворительного теоретического объяснения в предшествующих работах.
Проведенное исследование показало, что в противоположность предполагаемой
ранее эквивалентности J1 и
J2 [265], данные параметры
отличаются не только по величине, но и по знаку, а совокупность полученных
в работе значений параметров обменного взаимодействия между ближайшими
соседями по подрешетке V позволяет естественным образом воспроизвести
экспериментально наблюдаемую магнитную структуру в данном соединении (см.
рис. 6.7) без вовлечения в рассмотрение квантовых
флуктуационных эффектов, как это было сделано в [265].
Вычисленные в приближении LDA+U параметры межузельного обменного
взаимодействия можно использовать для расчета зависимости магнитной
восприимчивости от температуры 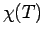 . Эта величина очень чувствительна
к обменным константам, и может быть измерена в эксперименте и рассчитана в
модели Гейзенберга квантовым методом Монте Карло (QMC) [266, 267]. В работе [16] было выполнено сравнение
экспериментальной зависимости
. Эта величина очень чувствительна
к обменным константам, и может быть измерена в эксперименте и рассчитана в
модели Гейзенберга квантовым методом Монте Карло (QMC) [266, 267]. В работе [16] было выполнено сравнение
экспериментальной зависимости 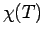 и вычисленной на основе LDA+U
параметров обменного взаимодействия; оно представлено на рис.
6.13.
и вычисленной на основе LDA+U
параметров обменного взаимодействия; оно представлено на рис.
6.13.
Рис. 6.13:
Сравнение рассчитанной методом QMC с LDA+U
параметрами обменного взаимодействия (таб. 6.2) и
измеренной в эксперименте температурной зависимости магнитной
восприимчивости для
CaV3O7.
|
|
В то время как наблюдается качественное согласие между вычисленной и
измеренной восприимчивостью, оно не столь хорошо в количественном
отношении, как это будет для остальных соединений исследуемой серии (см.
главу далее). Как объясняет автор расчетов кривой 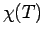 , это
происходит, по-видимому, из-за больших эффектов погашения при вычислениях
кривой, что увеличивает относительные ошибки расчета. Вполне вероятное
объяснение количественного несовпадения кривых можно дать с использованием
материалов работы [268]. Современные данные исследования
кристаллической структуры
CaV3O7
[268] свидетельствуют
о том, что параметры решетки и расстояния от атома ванадия до вершинного
кислорода несколько отличаются от тех, что были определены в [261, 260] и использованы в настоящих расчетах.
Можно
предположить, что LDA+U расчеты с новыми данными о кристаллической
структуре могли бы дать более хорошее количественное согласие обсуждаемых
кривых.
, это
происходит, по-видимому, из-за больших эффектов погашения при вычислениях
кривой, что увеличивает относительные ошибки расчета. Вполне вероятное
объяснение количественного несовпадения кривых можно дать с использованием
материалов работы [268]. Современные данные исследования
кристаллической структуры
CaV3O7
[268] свидетельствуют
о том, что параметры решетки и расстояния от атома ванадия до вершинного
кислорода несколько отличаются от тех, что были определены в [261, 260] и использованы в настоящих расчетах.
Можно
предположить, что LDA+U расчеты с новыми данными о кристаллической
структуре могли бы дать более хорошее количественное согласие обсуждаемых
кривых.
Исследованию величины и знака обменных взаимодействий в
CaV3O7
посвящены несколько работ [268, 269], вышедших после
опубликования в печати результатов, представленных в этом разделе. Так, в
[269] для этой цели используется метод
молекулярных орбиталей.
Авторы сделали вывод о том, что величина обменного взаимодействия между
пирамидами, соединенными вершинами, значительно больше, чем между
пирамидами, соединенными гранями; а в последних взаимодействие вдоль
направления b сильнее взаимодействия вдоль c. Их вывод полностью
совпал
с результатами, представленными здесь. В работе [268]
проведена подгонка разложения высокотемпературной серии 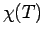 к
экспериментальной кривой. В этой работе приведены оценки (в наших
обозначениях) J1=45.2,
J2=-19.0,
J3=178.0 K,
что только для обмена
J3 не совпадает с изложенными здесь результатами
расчетов из ``первых
принципов''. Возможные причины несовпадения обменного параметра обсуждены в
предыдущем абзаце.
к
экспериментальной кривой. В этой работе приведены оценки (в наших
обозначениях) J1=45.2,
J2=-19.0,
J3=178.0 K,
что только для обмена
J3 не совпадает с изложенными здесь результатами
расчетов из ``первых
принципов''. Возможные причины несовпадения обменного параметра обсуждены в
предыдущем абзаце.
На основе сравнения поведения экспериментальной и теоретической кривой
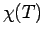 , а также результатов, полученных другими авторами и кратко
описанными выше, можно заключить, что результаты исследования электронной
структры соединения
CaV3O7
и параметров обменного взаимодействия
атомов V в нем достоверны. Они позволили впервые объяснить дальний
магнитный порядок в этом соединении и вычислить количественные
характеристики, годные для использования в дальнейших теоретических
исследованиях.
, а также результатов, полученных другими авторами и кратко
описанными выше, можно заключить, что результаты исследования электронной
структры соединения
CaV3O7
и параметров обменного взаимодействия
атомов V в нем достоверны. Они позволили впервые объяснить дальний
магнитный порядок в этом соединении и вычислить количественные
характеристики, годные для использования в дальнейших теоретических
исследованиях.
Электронная структура и обменные взаимодействия в
CaV2O5
и MgV2O5
Хотя
CaV2O5
и
MgV2O5
имеют почти одинаковые ванадий-кислородные
плоскости в основе своей кристаллической структуры, их магнитные свойства
заметно различны. Соединение
CaV2O5
имеет большую щель в магнонном
спектре порядка 600 K [270, 257, 271], а
спиновая щель в
MgV2O5
очень мала - только около 20 K [258, 272, 273] или, возможно, вообще отсутствует [271]. Дальнего магнитного порядка в
соединениях не
существует. В то время, когда представляемая работа только начиналась, было
неизвестно, в какой модели рассматривать данные соединения: то ли атомы
ванадия можно рассматривать как одномерные цепочки, то ли - как двумерные
лестницы со сравнимым взаимодействием вдоль ног и перекладин, то ли - как
димеры, состоящие из перекладин лестниц; знаки взаимодействий
(ферромагнитное или антиферромагнитное) были неизвестны также. Поэтому
представлялось необходимым провести неэмпирические расчеты обменных
взаимодействий в этих соединениях с целью понимания причин столь разного
значения спиновой щели.
Как подробно обсуждалось в разделе 6.1, основными
строительными
блоками кристаллической структуры соединений
Ca(Mg)V2O5
являются ионы
ванадия, каждый из которых находится примерно в центре пирамиды из пяти
кислородных ионов. Точечная группа для
V4+ -
C4v.
Пять d
орбиталей иона ванадия распадаются на следующие неприводимые представления:
3z2-r2 (A1),
x2-y2 (B1),
xy (B2) и (xz, yz) (E).
Орбиталью с
наинизшей энергией является орбиталь B2 (xy)
симметрии (причина этого -
расщепление кристаллическим полем вследствие специфического положения иона
ванадия внутри кислородной пирамиды - рассмотрена на стр.
![[*]](crossref.gif) ) в локальной системе координат, где ось z
направлена на
ближайший кислород (см. подробный разбор построения локальной системы
координат в разделе 6.2). Необходимо заметить, что
xy орбиталь
имеет малое перекрытие (
) в локальной системе координат, где ось z
направлена на
ближайший кислород (см. подробный разбор построения локальной системы
координат в разделе 6.2). Необходимо заметить, что
xy орбиталь
имеет малое перекрытие (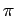 связь) с p орбиталями кислорода.
связь) с p орбиталями кислорода.
Расчет электронной структуры был проведен при следующем выборе радиусов
атомных сфер: 2.05 а.е. для ванадия, 2.30, 1.98, 1.62 а.е. для трех типов
кислорода, 3.19 а.е. для кальция, валентными орбиталями считались 4s,
4p, 3d для V и Ca, 2s, 2p, 3d для О.
Пять типов пустых сфер (10
штук на формульную единицу) были введены в элементарную ячейку для
заполнения объема. Результаты немагнитного расчета приведены на рис.
6.14.
Рис. 6.14:
Слева: полные плотности состояний на ячейку,
полученные в немагнитном расчете. В центре: соответствующая зонная
структра. Справа: зонная структура с выделенным вкладом от xy орбиталей
(fat bands). Верхний ряд: результаты расчета для
CaV2O5.
Нижний ряд
- для MgV2O5.
Уровень Ферми отмечен штриховыми линиями.
|
|
На этом рисунке зоны вычислены вдоль различных
симметричных направлений зон Бриллюэна, соответствующих примитивной
орторомбической (для
CaV2O5)
и базоцентрированной орторомбической (для
MgV2O5)
решеток (см. раздел 6.1). В обоих соединениях
зоны, расположенные ниже уровня Ферми до -3 эВ, сформированы, в основном,
2p состояниями кислорода и отделены от комплекса ванадиевых 3d
зон энергетической щелью. В интервале
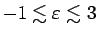 эВ
располагаются, в основном, ванадиевые 3d зоны. На рис.
6.14 в правом столбце показаны зоны,
соответствующие V xy
орбитали, так, что толщина каждой линии пропорциональна вкладу в зону V
xy состояний (ось x направлена вдоль перекладины лестницы,
а ось y -
вдоль ноги лестницы). Такой орбитальный анализ зон подтверждает , что
наинизшие 4 зоны в интервале
эВ
располагаются, в основном, ванадиевые 3d зоны. На рис.
6.14 в правом столбце показаны зоны,
соответствующие V xy
орбитали, так, что толщина каждой линии пропорциональна вкладу в зону V
xy состояний (ось x направлена вдоль перекладины лестницы,
а ось y -
вдоль ноги лестницы). Такой орбитальный анализ зон подтверждает , что
наинизшие 4 зоны в интервале
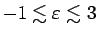 эВ
сформированы, в основном, V xy орбиталями. Расщепление кристаллическим
полем между xy орбиталями и остальными d орбиталями столь сильно
в немагнитном LDA расчете, особенно для
MgV2O5,
что xy зоны отделены
от остальных d зон небольшой энергетической щелью, как это видно из
полной плотности состояний, представленной на рис.
6.14
слева внизу. LDA+U расчет, выполненный с параметрами одноузельного
кулоновского взаимодействия U=3.6 и параметра Стонера
J=0.88 эВ, также приводит к выводу, что заполненными
орбиталями
являются орбитали типа xy (в локальных системах координат для каждого
атома ванадия) - рис. 6.15.
эВ
сформированы, в основном, V xy орбиталями. Расщепление кристаллическим
полем между xy орбиталями и остальными d орбиталями столь сильно
в немагнитном LDA расчете, особенно для
MgV2O5,
что xy зоны отделены
от остальных d зон небольшой энергетической щелью, как это видно из
полной плотности состояний, представленной на рис.
6.14
слева внизу. LDA+U расчет, выполненный с параметрами одноузельного
кулоновского взаимодействия U=3.6 и параметра Стонера
J=0.88 эВ, также приводит к выводу, что заполненными
орбиталями
являются орбитали типа xy (в локальных системах координат для каждого
атома ванадия) - рис. 6.15.
Рис. 6.15:
Вычисленное угловое распределение d электронной
спиновой плотности для двух атомов V, образующих перекладину лестницы, в
MgV2O5.
Сферы малого радиуса обозначают кислороды.
|
|
Оба соединения являются
изоляторами с величинами энергетической щели в 2.06 эВ в
CaV2O5
и 2.42 эВ в
MgV2O5;
значения спиновых магнитных моментов d оболочки
ионов V - 0.95  . Экспериментальным подтверждением вывода о
заполнении xy орбитали являются результаты работы [274] по
измерению сдвигов ЯМР на ядрах V в соединении
CaV2O5.
. Экспериментальным подтверждением вывода о
заполнении xy орбитали являются результаты работы [274] по
измерению сдвигов ЯМР на ядрах V в соединении
CaV2O5.
Для вычисления межузельных параметров обменного взаимодействия
Jij в
соответствии с формулами
(6.3) - (6.5) между двумя
подрешетками d атомов V элементарная ячейка
Ca(Mg)V2O5
была удвоена в плоскости (ab). Основываясь на вычислениях
знаков Jij между всеми
возможными парами ионов V из удвоенной элементарной ячейки при
ферромагнитном спиновом упорядочении, был сделан вывод о том, что реальная
магнитная структра является фрустрированной. Другими словами, невозможно
сконструировать такой дальний магнитный порядок, чтобы удовлетворить
вычисленным знакам обменных взаимодействий. Согласно выполненным расчетам,
обмен J1 между ближайшими соседями должен быть ферромагнитным в
CaV2O5
и антиферромагнитным в MgV2O5.
Все остальные ненулевые
обменные взаимодействия, включая взаимодействие вдоль перекладины лестницы
со вторым соседом J2, взаимодействие с третьими соседями J3 вдоль ноги
лестницы и взаимодействие вдоль диагонали лестницы J4, должны быть
антиферромагнитными. По-видимому, наилучшей моделью дальнего магнитного
порядка, описывающей с минимальными отклонениями реальную фрустрированную
магнитную структру
Ca(Mg)V2O5,
является та, что представлена на рис.
6.16.
Рис. 6.16:
Схема магнитных взаимодействий в соединениях
Ca(Mg)V2O5.
Показана элементарная ячейка, удвоенная в плоскости
(ab). Две ближайшие лестницы, образуемые атомами ванадия,
имеющими разные
координаты по оси c, представлены разной насыщенностью цвета. Дальний
магнитный порядок, использовавшийся в расчетах обменных взаимодействий,
показан стрелочками. Половина J1 и все J4 обменные взаимодействия
фрустрированы (имеют неправильный знак) в этой магнитной структуре.
|
|
Вычисленные значения межузельных параметров обменного взаимодействия
представлены в таб. 6.3.
Таб. 6.3:
Сравнение вычисленных межузельных обменных
взаимодействий (К) в
CaV2O5
и
MgV2O5.
Обозначение те же, что в
таб. 6.2.
| |
|
CaV2O5 |
MgV2O5 |
| |
|
xy-xy |
other |
total |
xy-xy |
other |
total |
| J1 |
между лестницами |
18 |
-64 |
-28 |
67 |
-74 |
60 |
| J2 |
вдоль перекладины |
295 |
18 |
608 |
42 |
8 |
92 |
| J3 |
вдоль ноги |
62 |
-2 |
122 |
71 |
2 |
144 |
| J4 |
вдоль диагонали |
10 |
0 |
20 |
10 |
-1 |
19 |
Наиболее сильное взаимодействие наблюдается между атомами, лежащими по одну
сторону плоскости (взаимодействия в лестнице J2 и J3). Если для
CaV2O5
обменные взаимодействия вдоль перекладины
(J2=608 K)
и вдоль ноги лестницы
(J3=122 K)
сильно анизотропны, то для
MgV2O5
те же значения
(J2=92 K и
J3=144 K) сравнимы по величине.
Представленные результаты позволяют рассматривать соединение
CaV2O5
как систему димеров, состоящих из перекладин с сильным взаимодействием,
слабо связанных вдоль ног лестниц. Этот вывод согласуется с результатами
работы [270], где температурная зависимость
магнитной
восприимчивости воспроизводилась моделью изолированных димеров с
J2=664 K.
Анализ, проведенный в работе [275] и основанный на
подгонке результатов модельных расчетов к экспериментально измеренной
кривой восприимчивости 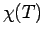 для
CaV2O5,
подтвердил предложенную
здесь картину слабо связанных димеров, и один из их наборов параметров
(J2=665 K,
J3=135 K,
J1=-25 K)
очень близок к параметрам, вычисленным
неэмпирическим путем и представляемым здесь. То же самое можно сказать и о
результатах работы [276], где подгоночные параметры оказались
равны
J2=655 K,
J3=93 K.
Приблизительно та же величина обмена в димере,
J2=640 K,
была получена при подгонке спектра рамановского рассеяния
CaV2O5
в работе [271] в модели
антиферромагнитной гейзенберговской S=1/2 двуножной
лестницы с
для
CaV2O5,
подтвердил предложенную
здесь картину слабо связанных димеров, и один из их наборов параметров
(J2=665 K,
J3=135 K,
J1=-25 K)
очень близок к параметрам, вычисленным
неэмпирическим путем и представляемым здесь. То же самое можно сказать и о
результатах работы [276], где подгоночные параметры оказались
равны
J2=655 K,
J3=93 K.
Приблизительно та же величина обмена в димере,
J2=640 K,
была получена при подгонке спектра рамановского рассеяния
CaV2O5
в работе [271] в модели
антиферромагнитной гейзенберговской S=1/2 двуножной
лестницы с
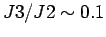 .
.
В то же время полученные отношения обменных взаимодействий в соединении
MgV2O5,
J2/J1=1.53 и
J3/J1=2.40,
уже не позволяют рассматривать
это соединение в модели спиновых лестниц. По своим свойствам оно скорее
уже находится на фазовой диаграмме, полученной в теории среднего поля
бозонов Швингера [277], в области спирально упорядоченной
бесщелевой фазы. При предположении о двумерном магнитном порядке была
оценена величина J3 из положения двухмагнонного пика на спектре
рамановского рассеяния в
MgV2O5
[271]. Это
оценочное значение, J3=180 K, очень близко к
вычисленному в настоящей работе.
Для соединений
Ca(Mg)V2O5
также была вычислена температурная
зависимость магнитной восприимчивости квантовым методом Монте Карло с
обменными взаимодействиями, приведенными в таб.
6.3.
Процедура расчетов подробно описана в [278]. Результаты расчета
приведены на рис. 6.17. Вследствие сильной
фрустрации
магнитной структуры теоретическая кривая не может быть продолжена в область
низких температур ниже максимума восприимчивости для
MgV2O5.
В то же время для
CaV2O5,
в котором обменное взаимодействие вдоль перекладины
J2 доминирует над остальными взаимодействиями, согласие теоретической и
экспериментальной кривыми наилучшее. Это является несомненным
доказательством правильности вычисленных параметров обменных
взаимодействий.
Рис. 6.17:
Сравнение рассчитанной методом QMC с LDA+U
параметрами обменного взаимодействия (таб. 6.3)
и измеренной в эксперименте температурной зависимости магнитной
восприимчивости для
CaV2O5
(a) и
MgV2O5
(b).
|
|
Теперь предстоит рассмотреть проблему, почему соединения
CaV2O5 и
MgV2O5
обладают столь различными свойствами. С химической точки
зрения можно предположить, что анизотропия обменных взаимодействий вдоль
перекладин и ног лестниц в
CaV2O5
и ее отсутствие в
MgV2O5
может быть следствием как химического состава соединений - в частности,
меньшего ионного радиуса Mg по сравнению с Ca, так и разницы в
кристаллической структуре этих материалов. Визуальное влияние последнего
фактора следует из рис. 6.18, где проекция на
VO5
пирамиды выбрана так, что два из четырех атомов кислорода, образующих
основание пирамиды, сливаются, а масштаб верхней и нижней части рисунка
одинаков. Явно видны различия кислородных пирамид, окружающих атомы ванадия
в обоих случаях. По-видимому, геометрия ближайшего окружения и играет
определяющую роль в наличии или отсутствии анизотропии обменных
взаимодействий для двух соединений.
Рис. 6.18:
Вычисленное угловое распределение d электронной
спиновой плотности для двух атомов V, образующих перекладину лестницы, в
MgV2O5
(вверху) и CaV2O5
(внизу). Верхний рисунок представляет
собой рис. 6.15 в иной проекции.
|
|
Для численного исследования влияния эффектов химического состава и различия
кристаллических структур дополнительно были рассчитаны обменные параметры
J2 и J3 для трех модельных соединений. Модель 1: В
соединении
CaV2O5
с реальной кристаллической структурой атом Ca заменен на атом
Mg для того, чтобы проверить, играет ли химический состав какую-либо роль в
анизотропии обменных взаимодействий. Для того чтобы выявить роль
кристаллической структуры, были рассмотрены следующие две модели.
Модель 2: Модель 1, в которой расстояния V-V и V-O изменены так, что они
стали равными соответствующим расстояниям в реальном соединении
MgV2O5
(см. таб. 6.1). Модель 3: Модель 2, в
которой и углы V-O-V изменены так, что они стали равны соответствующим
углам в реальном соединении
MgV2O5
(см. таб. 6.1). Более
подробное описание моделей и результаты расчета обменных взаимодействий
J2 и J3 приведены в таб. 6.4.
Таб. 6.4:
Данные кристаллической структуры для реальных соединений
CaV2O5
[260] и
MgV2O5
[258] и
трех модельных соединений, описанных в тексте, а также вычисленные обменные
взаимодействия вдоль перекладин J2 и ног лестниц J3 для всех пяти
модификаций.
| |
CaV2O5
|
Модель 1 |
| 1 |
Пространственная
группа |
Pmmn |
Pmmn |
| 2 |
Постоянные
решетки
(ангстремы) |
a=11.3512 |
a=11.3512 |
| b=3.6041 |
b=3.6041 |
| c=4.8931 |
c=4.8931 |
| 3 |
Позиции атомов |
V: (0.653884
0. 0.390610) |
V: (0.653884 0. 0.390610) |
| O1:
(0.62722 0. 0.06025) |
O1: (0.62722 0. 0.06025) |
| O2:
(0.82552 0. 0.46565) |
O2: (0.82552 0. 0.46565) |
| O3:
(0.50000 0. 0.54617) |
O3: (0.50000 0. 0.54617) |
| Ca:
(0.00000 0. 0.15592) |
Mg: (0.00000 0. 0.15592) |
| J2 (K) |
608 |
320 |
| J3 (K) |
122 |
92 |
| |
Модель 2 |
Модель 3 |
MgV2O5
|
| 1 |
Pmmn |
Pmmn |
Cmcm |
| 2 |
a=11.018 |
a=10.954706 |
a=3.692 |
| b=3.692 |
b=3.692 |
b=9.971 |
| c=4.9855 |
c=4.6900157 |
c=11.018 |
| 3 |
V:
(0.6530 0. 0.40388) |
V: (0.653884 0. 0.390610) |
V: (0.00000 0.20194 0.09700) |
| O1: (0.6225 0. 0.08640) |
O1: (0.621648 0. 0.048135) |
O1: (0.0000
0.0432 0.1275) |
| O2:
(0.8292 0. 0.47160) |
O2: (0.824254 0. 0.455768) |
O2: (0.0000 0.2358 -.0792) |
| O3: (0.5000 0. 0.60880) |
O3: (0.500000 0. 0.560822) |
O3: (0.0000
0.3044 0.2500) |
| Mg:
(0.0000 0. 0.22640) |
Mg: (0.000000 0. 0.189600) |
Mg: (0.0000 0.1132 0.7500) |
| J2 |
466 |
24 |
92 |
| J3 |
57 |
143 |
144 |
Из рассмотрения результатов, представленных в таб.
6.4, можно сделать следующие выводы.
Расчеты обменных
взаимодействий для модели 1 показывают, что простое изменение химического
состава, т.е. замена атома Ca атомом Mg, не влияет на анизотропию
взаимодействий вдоль перекладин и ног лестницы. Из расчетов модели 2 можно
заключить, что и длины связей V-V и V-O не определяют рассматриваемую
анизотропию. Однако расчеты для модели 3 однозначно демонстрируют, что как
только изменяются углы связи V-O-V, отношение обменных взаимодействий
существенно изменяется. В этой модели обмен вдоль перекладин становится
даже меньше обмена вдоль ног лестницы. При дальнейшем анализе результатов
таб. 6.4 становится понятным, что при переходе от
простой орторомбической упаковки VO5
пирамид к базоцентрированной
орторомбической упаковке восстанавливаются значения обменных параметров
J2 и J3, вычисленных для реальной кристаллической структуры
MgV2O5.
Итак, представленные расчеты обменных взаимодействий для
модельных кристаллических структур показывают, что разница в наклонах
VO5 пирамид
(таб. 6.1) и есть основная причина,
определяющая существенно различное магнитное поведение соединений
CaV2O5
и
MgV2O5.
Несколько слов о теоретических исследованиях магнитных свойств
MgV2O5
с использованием других механизмов их формирования. В недавней работе [279] справедливо было замечено, что
спин-орбитальное взаимодействие также может вносить свой вклад в формирование
магнитных свойств
MgV2O5.
В ней показано, что ион V4+ с
одним d
электроном может иметь почти немагнитное основное состояние под действием
кристаллического поля симметрии ниже, чем октаэдрической, в присутствии
спин-орбитального взаимодействия и некубических искажений. В этом случае
орбитальный момент может почти полностью скомпенсировать спиновый момент. В
общем необходимо подчеркнуть, что до сих пор соединение
MgV2O5
является наименее исследованным как в экспериментальном, так и
теоретическом плане из ряда всех рассматриваемых в данной главе сложных
оксидов ванадия
Ca(Mg)VnO2n+1.
Oбменные взаимодействия в
CaV4O9
Рис. 6.19:
Идеализированная кристаллическая структура атомов ванадия в
CaV4O9,
спроектированная на плоскость ab. Элементарная
ячейка размером
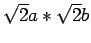 ограничена штрих-пунктирной линией.
Атомы ванадия, представленные в виде черных и белых кружков, имеют
различную координату по оси c.
ограничена штрих-пунктирной линией.
Атомы ванадия, представленные в виде черных и белых кружков, имеют
различную координату по оси c.
|
|
Прежде всего определим обозначения обменных взаимодействий, о которых
пойдет речь в последующем. Как указано в разделе 6.1 и
представлено на рис. 6.6 справа, в
CaV4O9
выделяют
два вида расположения атомов ванадия относительно друг друга: плакетки -
это атомы V, являющиеся вторыми соседями друг друга, попарно расположенные
по разные стороны от плоскости ab; и метаплакетки - это атомы V,
являющиеся третьими соседями друг друга, расположенные по одну сторону от
плоскости. Более подробное описание взаимодействий представлено на
рис. 6.19. Жирная черная линия обозначает связь между
ближайшими соседями, находящимися в разных метаплакетках, на расстоянии
2.99 ангстрем; соответствующий обмен обозначается как J1.
Сплошная тонкая
линия обозначает связь между вторыми соседями, находящимися в плакетках, на
расстоянии 3.01 ангстрем; соответствующий обмен вдоль сторон плакеток
обозначается как J2. Штриховая линия обозначает связь между третьими
соседями, находящимися в метаплакетках, на расстоянии 3.54 ангстрем;
соответствующий обмен вдоль сторон метаплакеток обозначается как J3. И,
наконец, пунктирная линия направлена вдоль диагонали плакеток, соединяя
атомы ванадия четвертых соседей на расстоянии 3.87 ангстрем;
соответствующий обмен вдоль диагоналей плакеток обозначается как J4.
В противоположность
MgV2O5,
соединение
CaV4O9
является наиболее
изученным. Первоначально было предложено, что щель в спектре магнонных
возбуждений порождается слабо связанными синглетными состояниями на четырех
плакетках спинов (в наших обозначениях речь шла о взаимодействии J2)
[280, 256,
281]. Совокупность этих четырех спиновых
синглетов получила название ``состояния резонансной валентной связи на
плакетках ванадия''. Позднее было предложено [255, 259],
что наибольшее взаимодействие наблюдается не в плакетках (J2), а в
метаплакетках (J3), и именно взаимодействие внутри метаплакетки
формирует
спиновую щель. Столь противоречивая ситуация была к моменту начала нашего
исследования.
Расчет электронной структуры был проведен при следующем выборе радиусов
атомных сфер: 2.05 а.е. для ванадия, 2.60, 2.08, 1.63 а.е. для трех типов
кислорода, 3.49 а.е. для кальция, валентными орбиталями считались 4s,
4p, 3d для V и Ca, 2s, 2p, 3d для О.
Четыре типа пустых сфер (10
штук на формульную единицу) были введены в элементарную ячейку для
заполнения объема. LDA+U расчет, выполненный с параметрами одноузельного
кулоновского взаимодействия U=3.6 и параметра Стонера
J=0.88 эВ, как и для других исследованных в этой главе
соединений
привел к результату, что заполненными орбиталями являются орбитали типа
xy (в локальных системах координат для каждого атома ванадия). Получен
энергетический спектр изоляторного типа с величиной энергетической щели в
2.48 эВ и значением спинового магнитного момента d оболочки ионов V -
0.95  . Основываясь на вычислениях знаков
Jij (формулы (6.3) -
(6.5)) между всеми возможными парами ионов V из
элементарной ячейки при ферромагнитном спиновом упорядочении, был сделан
вывод о том, что реальная магнитная структра является фрустрированной.
Другими словами, как и в случае
Ca(Mg)V2O5,
невозможно
сконструировать такой дальний магнитный порядок, чтобы удовлетворить
вычисленным знакам обменных взаимодействий. Согласно выполненным расчетам,
все обменные взаимодействия должны быть антиферромагнитными. По-видимому,
наилучшей моделью дальнего магнитного порядка, описывающей с минимальными
отклонениями реальную фрустрированную магнитную структру
CaV4O9,
является та, что представлена на рис. 6.20.
В этой модели
взаимодействие J4 имеет правильный знак (антиферромагнитное), и
половина взаимодействий J1-J3 также антиферромагнитно.
. Основываясь на вычислениях знаков
Jij (формулы (6.3) -
(6.5)) между всеми возможными парами ионов V из
элементарной ячейки при ферромагнитном спиновом упорядочении, был сделан
вывод о том, что реальная магнитная структра является фрустрированной.
Другими словами, как и в случае
Ca(Mg)V2O5,
невозможно
сконструировать такой дальний магнитный порядок, чтобы удовлетворить
вычисленным знакам обменных взаимодействий. Согласно выполненным расчетам,
все обменные взаимодействия должны быть антиферромагнитными. По-видимому,
наилучшей моделью дальнего магнитного порядка, описывающей с минимальными
отклонениями реальную фрустрированную магнитную структру
CaV4O9,
является та, что представлена на рис. 6.20.
В этой модели
взаимодействие J4 имеет правильный знак (антиферромагнитное), и
половина взаимодействий J1-J3 также антиферромагнитно.
Рис. 6.20:
Слева: схема дальнего магнитного порядка атомов
ванадия, использовавшегося в расчетах обменных взаимодействий в соединении
CaV4O9.
Кружки и квадраты обозначают атомы ванадия с различной
проекцией спина. Темные и светлые значки обозначают атомы ванадия, имеющие
различную координату по оси c. Справа для сравнения воспроизведен
рис. 6.19.
|
|
Таб. 6.5:
Рассчитанные параметры межузельного обменного
взаимодействия (К) в
CaV4O9.
Обозначение те же, что в таб. 6.2.
| |
xy-xy |
other |
total |
| J1 между
метаплакетками |
76 |
-90 |
62 |
| J2 вдоль стороны
плакетки |
73 |
-57 |
89 |
| J3 вдоль стороны
метаплакетки |
72 |
8 |
148 |
| J4 вдоль диагонали
плакетки |
45 |
1 |
91 |
Вычисленные значения параметров обменного взаимодействия представлены в
таб. 6.5. Вследствие того, что матрица
заселенности
атомов V с преимущественным заполнением xy орбиталей имеет ненулевые
недиагональные элементы, как это было подробно рассмотрено для случая
CaV3O7
на стр. ![[*]](crossref.gif) , в
CaV4O9
возникает существенный
ферромагнитный вклад в формирование обменных параметров J1 и J2.
Это приводит к уменьшению их абсолютного значения таким образом, что
преобладающим обменным взаимодействием становится J3 - взаимодействие
вдоль стороны метаплакетки, в соответствии с предположениями работ [255, 259].
Вместе с тем в отличие от результатов этих работ
представляемые результаты свидетельствуют о том, что взаимодействие J4
вдоль диагоналей плакетки сравнимо по величине с остальными
взаимодействиями.
, в
CaV4O9
возникает существенный
ферромагнитный вклад в формирование обменных параметров J1 и J2.
Это приводит к уменьшению их абсолютного значения таким образом, что
преобладающим обменным взаимодействием становится J3 - взаимодействие
вдоль стороны метаплакетки, в соответствии с предположениями работ [255, 259].
Вместе с тем в отличие от результатов этих работ
представляемые результаты свидетельствуют о том, что взаимодействие J4
вдоль диагоналей плакетки сравнимо по величине с остальными
взаимодействиями.
Полученные оценки J1-J4 могут объяснить порядок величины
спиновой щели в
CaV4O9.
Рассчитанная в рамках нефрустрированной J3-J4 модели,
щель в спектре спиновых возбуждений данного соединения при полученном
соотношении J3/J4=1.63 соответствует 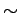 60 K [281] (экспериментальное
значение 107 K [282]). Однако, как показано в работе [283], учет фрустрации параметров J1
и J2 может привести к
увеличению данного значения, что позволяет ожидать значительно более
близкого к экспериметальному значения спиновой щели в рамках
фрустрированной модели. Еще один возможный способ проверки корректности
полученных величин J1-J4 - расчет дисперсии магнонного
спектра с этими параметрами, подобно тому, как это было выполнено в работе
[284]. Судя по их данным, полученном
на малом кластере, состоящим из
16 узлов, полученное нами отношение J3/J4 чуть
великовато для получения дисперсионного минимума в точке
(0,0), поэтому необходим расчет кластера
большего размера для уточнения отношения J3/J4.
На настоящий момент
использование рассчитанных значений обменных взаимодействий для
воспроизведения зависимости магнитной воспириимчивости от температуры
методом QMC (рис. 6.21) привело к хорошему
соответствию
теоретической и экспериментальной кривых, что свидетельствует о
правильности полученных результатов.
60 K [281] (экспериментальное
значение 107 K [282]). Однако, как показано в работе [283], учет фрустрации параметров J1
и J2 может привести к
увеличению данного значения, что позволяет ожидать значительно более
близкого к экспериметальному значения спиновой щели в рамках
фрустрированной модели. Еще один возможный способ проверки корректности
полученных величин J1-J4 - расчет дисперсии магнонного
спектра с этими параметрами, подобно тому, как это было выполнено в работе
[284]. Судя по их данным, полученном
на малом кластере, состоящим из
16 узлов, полученное нами отношение J3/J4 чуть
великовато для получения дисперсионного минимума в точке
(0,0), поэтому необходим расчет кластера
большего размера для уточнения отношения J3/J4.
На настоящий момент
использование рассчитанных значений обменных взаимодействий для
воспроизведения зависимости магнитной воспириимчивости от температуры
методом QMC (рис. 6.21) привело к хорошему
соответствию
теоретической и экспериментальной кривых, что свидетельствует о
правильности полученных результатов.
Рис. 6.21:
Сравнение рассчитанной методом QMC с LDA+U
параметрами обменного взаимодействия (таб. 6.5) и
измеренной в эксперименте температурной зависимости магнитной
восприимчивости для
CaV4O9.
|
|
Рис. 6.22:
Сравнение рассчитанной методом точной
диагонализации с параметрами обменного взаимодействия
(таб. 6.6) и измеренной в эксперименте
температурной зависимости магнитной восприимчивости для
CaV4O9.
Рисунок воспроизведен из работы [285].
|
|
Таб. 6.6:
Параметры межузельных обменного взаимодействия (мэВ) в
CaV4O9.
Первая строка: подгонка под экспериментальную кривую
(Fit). Вторая строка: извлеченные из данных по нейтронному рассеянию
(Neutron). Третья и четвертая строки: рассчитанные методами LSDA и SCAD.
Пятая строка: полученные в представляемой работе (LDA+U). Данные первых
четырех строк взяты из работы [285].
| Метод |
J1 |
J2 |
J3 |
J4 |
| Fit |
9.6 |
9.3 |
14.2 |
3.7 |
| Neutron |
6.8 |
6.8 |
14.0 |
1.7 |
| LSDA |
1.1 |
8.9 |
23.8 |
6.5 |
| SCAD |
12.5 |
9.7 |
19.3 |
3.9 |
| LDA+U |
5.3 |
7.7 |
12.8 |
7.8 |
Независимое от представленной работы и опубликованное на 3 месяца позже,
было выполнено подобное исследование обменных взаимодействий в
CaV4O9
[285] на основе расчетов в рамках
функционала спиновой
плотности (LSDA) и в модели самосогласованных атомных деформаций (SCAD).
Авторы также сравнивают свои результаты, обработанные в модели Гейзенберга
методом точной диагонализации, с экспериментальной кривой 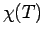 -
рис. 6.22. В таб. 6.6
в обозначениях, принятых в этой главе, сравниваются результаты расчета
обменных взаимодействий [285] с
представляемыми здесь. Как видно из
рис. 6.22 и таб. 6.6,
во всех случаях
наблюдается неплохое соответствие теоретических и экспериментальных кривых.
Таким образом, данные по обменным взаимодействиям, получаемые из
неэмпирических расчетов, позволяют корректно описывать физические
взаимодействия в системе
CaV4O9.
-
рис. 6.22. В таб. 6.6
в обозначениях, принятых в этой главе, сравниваются результаты расчета
обменных взаимодействий [285] с
представляемыми здесь. Как видно из
рис. 6.22 и таб. 6.6,
во всех случаях
наблюдается неплохое соответствие теоретических и экспериментальных кривых.
Таким образом, данные по обменным взаимодействиям, получаемые из
неэмпирических расчетов, позволяют корректно описывать физические
взаимодействия в системе
CaV4O9.
Выводы.
Основными результатами, полученными в этой главе, являются определение
заполненной орбитали (xy) и объяснение причин ее заполнения; выявление
главного фактора (изменение углов связи V-O-V), влияющего на различное
магнитное поведение соединений
MgV2O5
и
CaV2O5;
вычисление
величин и знаков межузельного обменного взаимодействия между ионами V в
исследуемых оксидах ванадия. Проведенные QMC расчеты магнитной
восприимчивости 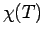 на основе LDA+U параметров межузельного обменного
взаимодействия для исследованного ряда соединений
Ca(Mg)VnO2n+1
показали, что вычисленное поведение
на основе LDA+U параметров межузельного обменного
взаимодействия для исследованного ряда соединений
Ca(Mg)VnO2n+1
показали, что вычисленное поведение 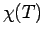 хорошо соответствует
экспериментальным данным. Это является еще одним подтверждением
правильности найденых из LDA+U расчета параметров межузельного обменного
взаимодействия для всего ряда оксидов. Итак, проведенное
исследование показало, что применение метода LDA+U позволяет как
качественно, так и количественно правильно описать электронное строение
слоистых оксидных соединений четырехвалентного ванадия, а также
интерпретировать их магнитные свойства с предсказанием знаков магнитных
взаимодействий.
хорошо соответствует
экспериментальным данным. Это является еще одним подтверждением
правильности найденых из LDA+U расчета параметров межузельного обменного
взаимодействия для всего ряда оксидов. Итак, проведенное
исследование показало, что применение метода LDA+U позволяет как
качественно, так и количественно правильно описать электронное строение
слоистых оксидных соединений четырехвалентного ванадия, а также
интерпретировать их магнитные свойства с предсказанием знаков магнитных
взаимодействий.
Результаты исследования электронной структуры и межузельных обменных
взаимодействий в соединениях ряда
Ca(Mg)VnO2n+1
были доложены
автором на семинарах отдела теоретической физики Института твердого тела
общества им. Макса Планка (Штутгарт, Германия, июнь 1998), физического
факультета Университета г. Оснабрюка (Германия, июль 1998), на XVII научной
школе-семинаре ``Рентгеновские и электронные спектры и химическая связь''
(Екатеринбург, 1999) [34], на 3-ем российско-германском семинаре
по электронной и рентгеновской спектроскопии (Екатеринбург, 1999) [35], на четвертом BUTSUKO симпозиуме по фазовому контролю в системах
со связанным спиновым, зарядовым и фотонным взаимодействием (Токио, Япония,
ноябрь 1999) [36], а также опубликованы в журналах ``Physical
Review Letters'' [16], ``Journal of Physics: Condensed Matter''
[17] и представлены в е-принте [278].
Следующая страница: Заключение
Предыдущая страница: Глава 5.
``Изменение орбитальной симметрии локализованного
3d1 электрона иона
V4+ при переходе
металл - изолятор в VO2''
Вернуться к содержанию диссертации
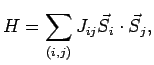
![]() взаимодействий вдоль
перекладин
взаимодействий вдоль
перекладин ![\includegraphics[width=0.525\textwidth]{Vanadates/mag.exc_cv4o9.eps}](img671.gif)
![]() орбитали электронная дырка приводит к сильному
орбитали электронная дырка приводит к сильному
![\includegraphics[width=0.575\textwidth]{Vanadates/cav2o5_cr.str.eps}](img673.gif)
![\includegraphics[width=0.325\textwidth,angle=0]{Vanadates/cav2o5_p1.eps}](img674.gif)
![\includegraphics[width=0.7\textwidth]{Vanadates/mgv2o5_cr.str.eps}](img675.gif)
![\includegraphics[width=0.55\textwidth]{Vanadates/camgv2o5_fig3.eps}](img677.gif)
![\includegraphics[width=0.575\textwidth]{Vanadates/cav3o7_cr.str.eps}](img684.gif)
![\includegraphics[width=0.4\textwidth,angle=0]{Vanadates/cav3o7_p.eps}](img685.gif)
![]() 30% расстояния от вершинного
кислорода до этой плоскости. В плоскости V-O есть вакансии. Если
представить идеализированную квадратную решетку атомов ванадия, в которой V
образует шахматную доску, то вакансии появляются на шахматной доске в
местах остановки коня. Атомы кальция расположены между слоями вместо
отсутствующих пирамид (рис. 6.5).
30% расстояния от вершинного
кислорода до этой плоскости. В плоскости V-O есть вакансии. Если
представить идеализированную квадратную решетку атомов ванадия, в которой V
образует шахматную доску, то вакансии появляются на шахматной доске в
местах остановки коня. Атомы кальция расположены между слоями вместо
отсутствующих пирамид (рис. 6.5).
![\includegraphics[width=0.41\textwidth]{Vanadates/cav4o9_cr.str.eps}](img691.gif)
![\includegraphics[width=0.45\textwidth,angle=0]{Vanadates/cav4o9_p.eps}](img692.gif)
![\includegraphics[width=0.45\textwidth]{Vanadates/mo_cv3o7.eps}](img695.gif)
![\includegraphics[clip=true,width=.975\textwidth]{Vanadates/cvoorb.eps}](img698.gif)
![]() ,
,
![]() ,
,
![]() ,
,
![]() и
и
![]() эВ. Установлено, что при смещении
иона V от основания пирамиды, не превышающем 10% ее высоты, наинизшим по
энергии является уровень, образованный состояниями yz и zx.
эВ. Установлено, что при смещении
иона V от основания пирамиды, не превышающем 10% ее высоты, наинизшим по
энергии является уровень, образованный состояниями yz и zx.
![\includegraphics[width=0.55\textwidth]{Vanadates/bonds_cv3o7.eps}](img707.gif)
![]() антиферромагнитное взаимодействие между ионами V из ближайших плакеток, в
то время как
антиферромагнитное взаимодействие между ионами V из ближайших плакеток, в
то время как ![]() связь ионов V внутри плакетки ожидается значительно
слабее (рис. 6.10). Однако нельзя
пренебрегать влиянием
двух геометрических факторов. Действительно, расстояние между ближайшими
атомами V, принадлежащими разным плакеткам, меньше, чем в одной и той же
плакетке (2.98 и 3.00 ангстрем против 3.53 ангстрем). С другой стороны, ионы V,
принадлежащие разным плакеткам, имеют существенно разную координату по оси
a, что ослабляет прямое dd перекрытие. Поэтому для того чтобы
исследовать взаимодействия между атомами V, необходим расчет параметров
обменного взаимодействия с учетом реальной кристаллической структуры
связь ионов V внутри плакетки ожидается значительно
слабее (рис. 6.10). Однако нельзя
пренебрегать влиянием
двух геометрических факторов. Действительно, расстояние между ближайшими
атомами V, принадлежащими разным плакеткам, меньше, чем в одной и той же
плакетке (2.98 и 3.00 ангстрем против 3.53 ангстрем). С другой стороны, ионы V,
принадлежащие разным плакеткам, имеют существенно разную координату по оси
a, что ослабляет прямое dd перекрытие. Поэтому для того чтобы
исследовать взаимодействия между атомами V, необходим расчет параметров
обменного взаимодействия с учетом реальной кристаллической структуры
![\includegraphics[width=0.5\textwidth]{Vanadates/cav3o7_pdos.eps}](img711.gif)


![]() , а матрица заселенности в этой локальной системе координат будет
выглядеть как:
, а матрица заселенности в этой локальной системе координат будет
выглядеть как:
![]() определяется в терминах
собственных функций
определяется в терминах
собственных функций ![]() и собственных значений
и собственных значений ![]() гамильтониана
метода
гамильтониана
метода ![]() (
(![]() равна 1, если
соответствующая
равна 1, если
соответствующая
![]() лежит не выше уровня
Ферми, и равна 0 в противоположном случае.
лежит не выше уровня
Ферми, и равна 0 в противоположном случае.
![]() и
и
![]() ,
где
,
где ![]() - интеграл межузельного перекрытия. Для рассматриваемых
соединений
- интеграл межузельного перекрытия. Для рассматриваемых
соединений
![\includegraphics[width=0.37\textwidth,angle=0]{Vanadates/defJ_cav3o7.eps}](img744.gif)
![]() . Эта величина очень чувствительна
к обменным константам, и может быть измерена в эксперименте и рассчитана в
модели Гейзенберга квантовым методом Монте Карло (QMC) [266, 267]. В работе [16] было выполнено сравнение
экспериментальной зависимости
. Эта величина очень чувствительна
к обменным константам, и может быть измерена в эксперименте и рассчитана в
модели Гейзенберга квантовым методом Монте Карло (QMC) [266, 267]. В работе [16] было выполнено сравнение
экспериментальной зависимости ![]() и вычисленной на основе
и вычисленной на основе ![\includegraphics[clip=true,width=.45\textwidth]{Vanadates/chi_cv3o7.eps}](img747.gif)
![]() , это
происходит, по-видимому, из-за больших эффектов погашения при вычислениях
кривой, что увеличивает относительные ошибки расчета. Вполне вероятное
объяснение количественного несовпадения кривых можно дать с использованием
материалов работы [268]. Современные данные исследования
кристаллической структуры
, это
происходит, по-видимому, из-за больших эффектов погашения при вычислениях
кривой, что увеличивает относительные ошибки расчета. Вполне вероятное
объяснение количественного несовпадения кривых можно дать с использованием
материалов работы [268]. Современные данные исследования
кристаллической структуры
![]() к
экспериментальной кривой. В этой работе приведены оценки (в наших
обозначениях)
к
экспериментальной кривой. В этой работе приведены оценки (в наших
обозначениях) ![]() , а также результатов, полученных другими авторами и кратко
описанными выше, можно заключить, что результаты исследования электронной
структры соединения
, а также результатов, полученных другими авторами и кратко
описанными выше, можно заключить, что результаты исследования электронной
структры соединения
![[*]](crossref.gif) ) в локальной системе координат, где ось z
направлена на
ближайший кислород (см. подробный разбор построения локальной системы
координат в разделе 6.2). Необходимо заметить, что
xy орбиталь
имеет малое перекрытие (
) в локальной системе координат, где ось z
направлена на
ближайший кислород (см. подробный разбор построения локальной системы
координат в разделе 6.2). Необходимо заметить, что
xy орбиталь
имеет малое перекрытие (![]() связь) с p орбиталями кислорода.
связь) с p орбиталями кислорода.
![\includegraphics[width=0.32\textwidth]{Vanadates/cav2o5_lda.dos.eps}](img757.gif)
![\includegraphics[width=0.32\textwidth]{Vanadates/cav2o5_lda.all_bnds.eps}](img758.gif)
![\includegraphics[width=0.32\textwidth]{Vanadates/cav2o5_lda.fat_bnds.eps}](img759.gif)
![\includegraphics[width=0.32\textwidth]{Vanadates/mgv2o5_lda.dos.eps}](img760.gif)
![\includegraphics[width=0.32\textwidth]{Vanadates/mgv2o5_lda.all_bnds.eps}](img761.gif)
![\includegraphics[width=0.32\textwidth]{Vanadates/mgv2o5_lda.fat_bnds.eps}](img762.gif)
![]() эВ
располагаются, в основном, ванадиевые 3d зоны. На рис.
6.14 в правом столбце показаны зоны,
соответствующие V xy
орбитали, так, что толщина каждой линии пропорциональна вкладу в зону V
xy состояний (ось x направлена вдоль перекладины лестницы,
а ось y -
вдоль ноги лестницы). Такой орбитальный анализ зон подтверждает , что
наинизшие 4 зоны в интервале
эВ
располагаются, в основном, ванадиевые 3d зоны. На рис.
6.14 в правом столбце показаны зоны,
соответствующие V xy
орбитали, так, что толщина каждой линии пропорциональна вкладу в зону V
xy состояний (ось x направлена вдоль перекладины лестницы,
а ось y -
вдоль ноги лестницы). Такой орбитальный анализ зон подтверждает , что
наинизшие 4 зоны в интервале
![]() эВ
сформированы, в основном, V xy орбиталями. Расщепление кристаллическим
полем между xy орбиталями и остальными d орбиталями столь сильно
в немагнитном LDA расчете, особенно для
эВ
сформированы, в основном, V xy орбиталями. Расщепление кристаллическим
полем между xy орбиталями и остальными d орбиталями столь сильно
в немагнитном LDA расчете, особенно для
![\includegraphics[clip=true,width=.55\textwidth]{Vanadates/camgv2o5_fig4.eps}](img765.gif)
![]() . Экспериментальным подтверждением вывода о
заполнении xy орбитали являются результаты работы [274] по
измерению сдвигов ЯМР на ядрах V в соединении
. Экспериментальным подтверждением вывода о
заполнении xy орбитали являются результаты работы [274] по
измерению сдвигов ЯМР на ядрах V в соединении
![\includegraphics[clip=true,width=.35\textwidth]{Vanadates/camgv2o5_fig1.eps}](img771.gif)
![]() для
для
![]() .
.
![\includegraphics[clip=true,width=.9\textwidth]{Vanadates/chi_cmv2o5.eps}](img787.gif)
![\includegraphics[clip=true,width=.425\textwidth]{Vanadates/camgv2o5_rung_orb.eps}](img788.gif)
![\includegraphics[width=0.35\textwidth,angle=0]{Vanadates/defJ_cav4o9.eps}](img790.gif)
![]() . Основываясь на вычислениях знаков
. Основываясь на вычислениях знаков
![\includegraphics[clip=true,width=.35\textwidth]{Vanadates/cav4o9_ms4.eps}](img792.gif)
![\includegraphics[clip=true,width=0.35\textwidth]{Vanadates/defJ_cav4o9.eps}](img793.gif)
![[*]](crossref.gif) , в
, в
![]() 60 K [281] (экспериментальное
значение 107 K [282]). Однако, как показано в работе [283], учет фрустрации параметров J1
и J2 может привести к
увеличению данного значения, что позволяет ожидать значительно более
близкого к экспериметальному значения спиновой щели в рамках
фрустрированной модели. Еще один возможный способ проверки корректности
полученных величин
60 K [281] (экспериментальное
значение 107 K [282]). Однако, как показано в работе [283], учет фрустрации параметров J1
и J2 может привести к
увеличению данного значения, что позволяет ожидать значительно более
близкого к экспериметальному значения спиновой щели в рамках
фрустрированной модели. Еще один возможный способ проверки корректности
полученных величин ![\includegraphics[clip=true,width=.45\textwidth]{Vanadates/chi_cv4o9.eps}](img800.gif)
![\includegraphics[clip=true,width=.45\textwidth]{Vanadates/chi_Hellberg.eps}](img801.gif)
![]() -
рис. 6.22. В таб. 6.6
в обозначениях, принятых в этой главе, сравниваются результаты расчета
обменных взаимодействий [285] с
представляемыми здесь. Как видно из
рис. 6.22 и таб. 6.6,
во всех случаях
наблюдается неплохое соответствие теоретических и экспериментальных кривых.
Таким образом, данные по обменным взаимодействиям, получаемые из
неэмпирических расчетов, позволяют корректно описывать физические
взаимодействия в системе
-
рис. 6.22. В таб. 6.6
в обозначениях, принятых в этой главе, сравниваются результаты расчета
обменных взаимодействий [285] с
представляемыми здесь. Как видно из
рис. 6.22 и таб. 6.6,
во всех случаях
наблюдается неплохое соответствие теоретических и экспериментальных кривых.
Таким образом, данные по обменным взаимодействиям, получаемые из
неэмпирических расчетов, позволяют корректно описывать физические
взаимодействия в системе
![]() на основе
на основе ![]() хорошо соответствует
экспериментальным данным. Это является еще одним подтверждением
правильности найденых из
хорошо соответствует
экспериментальным данным. Это является еще одним подтверждением
правильности найденых из