Следующая страница:
Глава 4.
``CrO2 - самолегированный
ферромагнетик с механизмом двойного обмена''
Предыдущая страница:
Глава 2. ``Исследование причин упорядочения занятых
eg орбиталей ионов
Mn3+ в манганитах
Pr1-xCaxMnO3
(x=0 и
x=1/2) и
La7/8Sr1/8MnO3''
Вернуться к содержанию диссертации
Параграфы:
Глава 3.
Состояние ионов Co3+ с
промежуточным спином в LaCoO3
Среди оксидных систем, имеющих переход полупроводник - металл, кобальтит
лантана LaCoO3 особенно
интересен из-за своего очень необычного
магнитного поведения. При повышении температуры по достижении 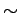 90 K
происходит переход от немагнитного к парамагнитному полупроводнику, а при
90 K
происходит переход от немагнитного к парамагнитному полупроводнику, а при
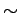 500 K наблюдается переход полупроводник - металл.
Несмотря на то, что
большое количество исследований было проведено с начала 1960-х годов,
характер перехода и природа температурной зависимости спинового состояния
до сих пор не ясны. Например, температурная зависимость магнитной
восприимчивости имеет пик около 90 K, после которого при повышении
температуры следует спад магнитной восприимчивости по закону
Кюри - Вейсса [125], что интерпретировалось как переход ионов
Co3+ из низкоспинового
(НС) в высокоспиновое (ВС)
состояние
500 K наблюдается переход полупроводник - металл.
Несмотря на то, что
большое количество исследований было проведено с начала 1960-х годов,
характер перехода и природа температурной зависимости спинового состояния
до сих пор не ясны. Например, температурная зависимость магнитной
восприимчивости имеет пик около 90 K, после которого при повышении
температуры следует спад магнитной восприимчивости по закону
Кюри - Вейсса [125], что интерпретировалось как переход ионов
Co3+ из низкоспинового
(НС) в высокоспиновое (ВС)
состояние![[*]](footnote.gif) . Переход полупроводник - металл
происходит в диапазоне температур 400-600 K - значительно выше магнитного
перехода. Природу того, что
LaCoO3 оказывается полупроводником
ниже
400-600 K, Раках и Гудинаф связывали с упорядочением НС и ВС ионов Co3+
в структуре типа NaCl [126, 127, 128, 129] с делокализованными
электронами в широкой зоне, образуемой
eg орбиталями
переходного
металла. Однако подобное изменение структуры не наблюдалось в
экспериментах. Эксперименты по рассеянию нейтронов [130]
предполагают, что переход полупроводник - металл не сопровождается
существенным изменением магнитных характеристик, но ясная картина природы
перехода в LaCoO3 отсутствует.
. Переход полупроводник - металл
происходит в диапазоне температур 400-600 K - значительно выше магнитного
перехода. Природу того, что
LaCoO3 оказывается полупроводником
ниже
400-600 K, Раках и Гудинаф связывали с упорядочением НС и ВС ионов Co3+
в структуре типа NaCl [126, 127, 128, 129] с делокализованными
электронами в широкой зоне, образуемой
eg орбиталями
переходного
металла. Однако подобное изменение структуры не наблюдалось в
экспериментах. Эксперименты по рассеянию нейтронов [130]
предполагают, что переход полупроводник - металл не сопровождается
существенным изменением магнитных характеристик, но ясная картина природы
перехода в LaCoO3 отсутствует.
Результаты других экспериментальных исследований - рентгеновской
фотоэмиссии и рентгеновского поглощения - интерпретировались как изменения
в системе спинов при переходе полупроводник - металл [131]. Но и в
таком рассмотрении есть некоторая несогласованность. Линия Co 2p спектра
фотоэмиссии при комнатной температуре имеет форму, соответствующую иону
Co3+ в НС состоянии,
что не согласуется со спиновым
переходом при 90 K. Также, валентная полоса спектра поглощения при
300 K
совершенно отличается от полосы ВС состояния. Таким образом,
интерпретация двух переходов до сих пор неочевидна.
Рис. 3.1:
Схема энергетических уровней для низкоспинового
состояния в LaCoO3 (по работам [126, 127, 128, 129]).
|
В большинстве предшествующих исследований состояния ионов Co
рассматривались на основе ионной картины. Первую модель для объяснения
перехода в LaCoO3 предложил
и развил Гудинаф [126, 127, 128, 129]. Было предложено, что для
трехвалентного Co в LaCoO3
энергия кристаллического поля
 только незначительно больше, чем энергия внутриатомного обмена
только незначительно больше, чем энергия внутриатомного обмена
 (рис. 3.1). В
такой модели основное
состояние ионов Co - НС (
(рис. 3.1). В
такой модели основное
состояние ионов Co - НС ( , S=0), а возбужденное -
ВС состояние (
, S=0), а возбужденное -
ВС состояние ( , S=2) - только на 0.08 эВ выше по
энергии
, S=2) - только на 0.08 эВ выше по
энергии![[*]](footnote.gif) . Увеличение температуры приводит к заполнению
ВС состояния, что и отражается в измерениях магнитной
восприимчивости. Переход полупроводник - металл интерпретировался
качественно как образование широкой
. Увеличение температуры приводит к заполнению
ВС состояния, что и отражается в измерениях магнитной
восприимчивости. Переход полупроводник - металл интерпретировался
качественно как образование широкой  зоны из локализованных
ионных eg состояний.
Предполагался дальний порядок НС и
ВС ионов Co, основанный на результатах измерений рентгеновской
дифракции. Эксперименты по нейтронной дифракции [130] не
подтвердили этот дальний порядок, но также и не опровергли возможный
ближний порядок.
зоны из локализованных
ионных eg состояний.
Предполагался дальний порядок НС и
ВС ионов Co, основанный на результатах измерений рентгеновской
дифракции. Эксперименты по нейтронной дифракции [130] не
подтвердили этот дальний порядок, но также и не опровергли возможный
ближний порядок.
Теоретическое описание LaCoO3
является сложной задачей из-за того, что в
системе наблюдается переход от локализованного к делокализованному
поведению, и два основных существующих метода - вычисления
одноэлектронной зонной структуры в приближении локальной электронной
плотности (LDA) и ``конфигурационное взаимодействие модельного
гамильтониана'' (которые оба использовались при рассмотрении
LaCoO3 [131, 132]) - были сконструированы для
совершенно нелокализованных и полностью локализованных случаев,
соответственно.
В работе [56] представлены результаты
вычислений в приближении
локальной спиновой плотности (LSDA) для
LaMO3
(M=Mn, Fe, Co, Ni). Там
было отмечено, что результаты LSDA имеют хорошее согласие с рентгеновскими
фотоэмиссионными спектрами. Такое согласие не является необходимым
доказательством адекватного описания электронной структуры. Хорошо
известный пример - NiO, где LSDA дает острый пик на потолке валентной зоны
в соответствии с фотоэмиссионными спектрами, но природа пика в этом случае
- 3d t2g состояния
Ni со спином вниз, в то время как общепринято,
что этот пик образуется из конечного состояния
 . Реальным
доказательством правильности одноэлектронного приближения было бы
отсутствие сателлитов в фотоэмиссионном спектре. Также фотоэмиссионные
спектры, с которыми проводилось сравнение в [56], были получены
при комнатной температуре, при которой
LaCoO3 находится не в
НС состоянии. Таким образом, эти фотоэмиссионные спектры данные нужно
сравнивать с LSDA результатами, соответствующими магнитному решению, а не
немагнитному, как в работе [56].
. Реальным
доказательством правильности одноэлектронного приближения было бы
отсутствие сателлитов в фотоэмиссионном спектре. Также фотоэмиссионные
спектры, с которыми проводилось сравнение в [56], были получены
при комнатной температуре, при которой
LaCoO3 находится не в
НС состоянии. Таким образом, эти фотоэмиссионные спектры данные нужно
сравнивать с LSDA результатами, соответствующими магнитному решению, а не
немагнитному, как в работе [56].
Mетод LDA+U, который совмещает в одной вычислительной схеме
подходы LDA и
модели Хаббарда, позволяет исследовать системы с сильными кулоновскими
корреляциями на основе ``первых принципов'' (без подгоночных параметров).
Этот метод (в отличие от стандартного LDA) может описать существование
различных состояний системы, которые близки по полной энергии. Например, в
этом приближении можно рассматривать состояние с промежуточным спином
(ПС), которое приводит к понижению локальной симметрии ионов Co и
орбитальному упорядочению. Как известно, оксиды с высокой формальной
степенью окисления принадлежат к системам с отрицательной энергией
зарядового переноса в схеме Заанена - Саватcкого - Аллена [133]
(более подробно эта схема изложена в параграфе
4.3), что
может привести к существенной модификации электронной структуры, в
особенности, к возможной стабилизации ПС состояния [134].
В этом разделе представлено теоретическое исследование электронной
структуры LaCoO3 методом
LDA+U. В отличие от стандартного LDA, в LDA+U
существует несколько стабильных решений, соответствующих различным
локальным минимумам функционала LDA+U. В результате проделанных расчетов
было получено, что основное состояние оказалось немагнитным, что
согласуется с экспериментом. Обнаружено также два орбитально поляризованных
магнитных решения, соответствующих ПС состоянию (одно из которых
бесщелевой полупроводник, а другое металл), и магнитное решение
(полупроводник), соответствующие ВС состоянию, которое лежит
значительно выше по энергии. Дополнительно получено, что
eg состояния
образуют широкие зоны, в то время как зоны
t2g состояний узкие,
расщепленные кулоновским взаимодействием на нижнюю (занятую) и верхнюю
(пустую) хаббардовские зоны. Используя результаты этих вычислений,
предложена интерпретация поведения
LaCoO3. В соответствии с
этой схемой
при увеличении температуры сначала происходит переход из НС
(немагнитного) полупроводникового основного состояния в ПС состояние
(конфигурация
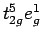 ). Из-за сильной ян - теллеровской природы этой
конфигурации в этом состоянии может произойти орбитальное упорядочение.
Состояние с орбитальным порядком в наших вычислениях оказалось
неметаллическим (в действительности полупроводник с практически нулевой
щелью). С дальнейшим увеличением температуры орбитальное упорядочение может
постепенно разрушаться, что может объяснить переход в металлическое
состояние в LaCoO3 при
400-600 K. Мы надеемся, что эта информация в
конечном итоге приведет к лучшему пониманию
LaCoO3 и других похожих
материалов.
). Из-за сильной ян - теллеровской природы этой
конфигурации в этом состоянии может произойти орбитальное упорядочение.
Состояние с орбитальным порядком в наших вычислениях оказалось
неметаллическим (в действительности полупроводник с практически нулевой
щелью). С дальнейшим увеличением температуры орбитальное упорядочение может
постепенно разрушаться, что может объяснить переход в металлическое
состояние в LaCoO3 при
400-600 K. Мы надеемся, что эта информация в
конечном итоге приведет к лучшему пониманию
LaCoO3 и других похожих
материалов.
Рис. 3.2:
Элементарная ячейка LaCoO3
(пунктирная линия),
содержащая два атома Co (шары) в окружении кислородных октаэдров. |
Приближение LDA+U было применено к вычислительной схеме
линеаризованных
маффин-тин (MT) орбиталей с полным потенциалом (FP LMTO) [135, 136]. Кристаллографические данные,
использовавшиеся в вычислениях, были взяты из [130]. В соответствии с ними
LaCoO3 имеет структуру
псевдокубического перовскита с ромбоэдрическим
искажением вдоль направления (111) (рис. 3.2).
Элементарная ячейка содержит две формульных единицы. Так как
ромбоэдрическое искажение мало (наибольший ромбоэдрический угол
60.990o при 4 K), в дальнейшем для
интерпретации полученных
результатов мы используем представление
t2g и
eg орбиталей.
Температура в наших вычислениях была введена только посредством изменения
параметра решетки и ромбоэдрического угла в соответствии с данными из [130]. Наиболее детальное описание
технических аспектов вычислений
методом FP LMTO для сложных оксидов структуры перовскита могут быть
найдены в [137]. Оптимальный выбор
базисного набора для описания валентной зоны и дна зоны проводимости
представлен в таблице 3.1.
Таб. 3.1:
Базисный набор и радиусы MT-сфер, использованные в вычислениях.
| Атом |
 Ry Ry |
 Ry Ry |
 Ry Ry |
RMT |
| La |
6s6p5d4f |
6s6p5d4f |
6s6p5d |
1.77 |
| Co |
4s4p3d |
4s4p3d |
4s4p |
1.26 |
| O |
2s2p |
2s2p |
2s |
0.66 |
|
Величины одноузельного кулоновского U и внутриатомного
обменного взаимодействий J были вычислены с использованием процедуры
сверхъячейки [84] U=7.8 эВ и
J=0.92 эВ. Так как U поправка
применяется к d орбиталям Co, значение радиуса MT сфер Co было выбрано
близким к его значению в металлическом Co для того, чтобы получить полную
d плотность внутри сферы. Для правильного описания волновой функции в
межсферной области мы раскладывали сферические гармоники до значения
lmax=5, 4, 3 для La, Co и O MT сфер,
соответственно. Интегрирование по
зоне Бриллюэна в процессе самосогласования выполнялось по 65 k точкам
в неприводимой части зоны Бриллюэна. Плотности состояний были вычислены
методом тетраэдров по 739 k точкам в полной зоне Бриллюэна. Так как в
LDA+U потенциалы для различных d орбиталей Co различны,
a priori неочевидно, какова будет симметрия конечного состояния
рассматриваемой системы. В предварительных вычислениях для простоты было
предположено, что LaCoO3
имеет идеальную кубическую структуру типа
перовскитa. Для того, чтобы позволить системе самой выбрать симметрию,
интегрирование проводилось не по
1/48 части зоны Бриллюэна,
как для кубической симметрии, а по
1/8 (группа симметрии
D2h.
В результате была получена кубическая симметрия
Oh для основного
(НС) состояния, и тетрагональная
D4h для возбужденных
состоянии. Практически то же самое происходит в реальной симметрии
 : заселенности орбиталей xy, yz и
zx примерно одинаковы
для НС конфигурации, также как и заселенности орбиталей
3z2-r2 и
x2-y2.
Вырождение xy, yz и zx
снимается в других спиновых состояниях.
: заселенности орбиталей xy, yz и
zx примерно одинаковы
для НС конфигурации, также как и заселенности орбиталей
3z2-r2 и
x2-y2.
Вырождение xy, yz и zx
снимается в других спиновых состояниях.
Этот раздел посвящен изложению результатов вычислений для однородных
режимов без дополнительной сверхструктуры. Возможность получения результата
с орбитальным упорядочением рассматривается в
разделе 3.3.
Детальные результаты вычислений с кристаллографическими данными,
соответствующими 4 K, приведены в
таблице 3.2.
Таб. 3.2:
Вычисленные заселенности d орбиталей Co,
спиновые магнитные моменты, характер энергетического спектра и разница
полной энергии  относительно энергии
относительно энергии
 конфигурации
для различных спиновых состояний ионов Co в
LaCoO3.
конфигурации
для различных спиновых состояний ионов Co в
LaCoO3.
конфи-
гурация |
спин |
d-заселенности |

( ) ) |
щель (эВ) |
 (эВ) (эВ) |
| xy |
yz |
zx |
3z2-r2 |
x2-y2 |
сумма |
 ,HC ,HC |
 , ,
 |
0.98 |
0.98 |
0.99 |
0.32 |
0.33 |
7.20 |
0 |
2.06 |
- |
 ,ПС ,ПС |
 |
0.98 |
0.98 |
0.98 |
0.84 |
0.84 |
7.13 |
2.11 |
нет |
0.24 |
 |
0.07 |
0.98 |
0.99 |
0.23 |
0.24 |
 ,BC ,BC |
 |
0.99 |
0.99 |
0.99 |
1.00 |
1.00 |
6.78 |
3.16 |
0.13 |
0.65 |
 |
0.99 |
0.08 |
0.11 |
0.33 |
0.30 |
 Полуметалл. Энергетическая щель
присутствует только для электронов со спином вниз.
Полный магнитный момент на элементарную ячейку равен 2 Полуметалл. Энергетическая щель
присутствует только для электронов со спином вниз.
Полный магнитный момент на элементарную ячейку равен 2  . . |
|
Для получения НС конфигурации необходимо стартовать процесс
самосогласования с равных заселенностей всех трех
t2g орбиталей и двух
eg орбиталей
(например,
 ). Начальная спиновая поляризация
исчезает в процессе самосогласования, что в результате приводит к
немагнитному решению. Спектр зарядовых возбуждений имеет полупроводниковый
характер в соответствии с экспериментальными данными [138] (и
в противоположность результату LDA [132]) со щелью, равной
2.06 эВ. Вершина валентной зоны
(рис. 3.3) состоит из смеси 2p
кислородных состояний и
t2g состояний Co,
а дно зоны проводимости
образуется главным образом
eg состояниями Co.
). Начальная спиновая поляризация
исчезает в процессе самосогласования, что в результате приводит к
немагнитному решению. Спектр зарядовых возбуждений имеет полупроводниковый
характер в соответствии с экспериментальными данными [138] (и
в противоположность результату LDA [132]) со щелью, равной
2.06 эВ. Вершина валентной зоны
(рис. 3.3) состоит из смеси 2p
кислородных состояний и
t2g состояний Co,
а дно зоны проводимости
образуется главным образом
eg состояниями Co.
Рис. 3.3:
Полная и парциальные плотности состояний, полученные в
LDA+U расчете
для LaCoO3 c ионами Co в
низкоспиновом состоянии ( конфигурация). Для парциальных плотностей состояний d-Co сплошная
линия обозначает вклад
t2g орбиталей,
а штриховая линия - eg
орбиталей.
конфигурация). Для парциальных плотностей состояний d-Co сплошная
линия обозначает вклад
t2g орбиталей,
а штриховая линия - eg
орбиталей.
|
Из рентгеновских спектров эмиссии и поглощения [131] значение
щели оценивалось как 0.9 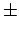 0.3 эВ. Оптические измерения [139]
дают
0.3 эВ. Оптические измерения [139]
дают  эВ. Большее значение щели, полученное из вычислений,
может быть объяснено хорошо известным фактом, что приближение среднего
поля, которое является основой метода LDA+U, обычно переоценивает
тенденцию к локализации и, таким образом, значение щели.
эВ. Большее значение щели, полученное из вычислений,
может быть объяснено хорошо известным фактом, что приближение среднего
поля, которое является основой метода LDA+U, обычно переоценивает
тенденцию к локализации и, таким образом, значение щели.
Целью данных исследований является нахождение решений, соответствующих
более высоким спиновым состояниям. Обычно высокоспиновое состояние
описывается как конфигурация
 с максимальным значением спина
S=2 (магнитный момент
с максимальным значением спина
S=2 (магнитный момент  =4
=4  ). Это соответствует чисто ионной
модели, а гибридизация 3d орбиталей Co с кислородными 2p
орбиталями и
образование зон в твердом теле могут значительно изменить это ионное
значение. Такая ренормализация была получена в наших вычислениях
(таблица 3.2).
Начальная конфигурация
). Это соответствует чисто ионной
модели, а гибридизация 3d орбиталей Co с кислородными 2p
орбиталями и
образование зон в твердом теле могут значительно изменить это ионное
значение. Такая ренормализация была получена в наших вычислениях
(таблица 3.2).
Начальная конфигурация
 (две
дырки на орбиталях
(две
дырки на орбиталях
 ,
,
 из
t2g
набора и две на
из
t2g
набора и две на
 ,
,
 из
набора eg) приходит к
самосогласованному решению с магнитным моментом
из
набора eg) приходит к
самосогласованному решению с магнитным моментом
 =3.16
=3.16  . Полная энергия этого ВС решения на
0.65 эВ (в расчете на одну формульную единицу) выше, чем НС
конфигурация
. Полная энергия этого ВС решения на
0.65 эВ (в расчете на одну формульную единицу) выше, чем НС
конфигурация
 основного состояния. Оказалось, что существует
решение с промежуточным спином
(вторая строчка в таблице 3.2,
значение магнитного момента
основного состояния. Оказалось, что существует
решение с промежуточным спином
(вторая строчка в таблице 3.2,
значение магнитного момента
 =2.11
=2.11  ),
которое ниже по полной энергии, чем ВС решение (0.24 эВ в расчете
на одну формульную единицу относительно основного состояния НС).
Это решение было получено, когда старт процесса самосогласования происходил
из начальной конфигурации
),
которое ниже по полной энергии, чем ВС решение (0.24 эВ в расчете
на одну формульную единицу относительно основного состояния НС).
Это решение было получено, когда старт процесса самосогласования происходил
из начальной конфигурации
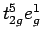 , когда только один электрон был
перенесен из t2g в
eg состояния.
Конечная самосогласованная
конфигурация лучше описывается как состояние
, когда только один электрон был
перенесен из t2g в
eg состояния.
Конечная самосогласованная
конфигурация лучше описывается как состояние  с частично
заполненной
с частично
заполненной  зоной (
зоной ( ) с заселенностями
) с заселенностями
 и
и
 , равными 0.84. На языке
конфигурационного взаимодействия, используемого в кластерных расчетах, это
можно сравнить с состоянием
, равными 0.84. На языке
конфигурационного взаимодействия, используемого в кластерных расчетах, это
можно сравнить с состоянием
 , где
, где
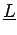 обозначает дырку в 2p состояниях кислорода.
обозначает дырку в 2p состояниях кислорода.
Состояние ПС в вычислениях оказалось металлическим (см. однако
раздел 3.3), а состояние ВС -
полупроводящим
(рис. 3.4 и 3.5).
Причина этого заключается в том, что
антисвязывающая  зона, образуемая
зона, образуемая
 орбиталями,
очень широкая, и расщепление зон недостаточно сильно, чтобы образовать
энергетическую щель в случае ПС состояния. Щель между полностью
заполненной
орбиталями,
очень широкая, и расщепление зон недостаточно сильно, чтобы образовать
энергетическую щель в случае ПС состояния. Щель между полностью
заполненной
 и полностью пустой
и полностью пустой
 зонами
появляется в ВС состоянии.
зонами
появляется в ВС состоянии.
Рис. 3.4:
Полная и парциальные плотности состояний,
полученные в LDA+U расчете
для LaCoO3 с ионами Co в
состоянии с промежуточным спином
(конфигурация
 ). Уровень Ферми обозначен
вертикальной штриховой линией. Стрелки соответствуют проекциям
спина вверх и вниз. Обозначения те же, что и на
рис. 3.3
). Уровень Ферми обозначен
вертикальной штриховой линией. Стрелки соответствуют проекциям
спина вверх и вниз. Обозначения те же, что и на
рис. 3.3 |
Рис. 3.5:
Полная и парциальные плотности состояний,
полученные в LDA+U расчете
для LaCoO3 с ионами Co
в высокоспиновом состоянии (конфигурация
 ). Уровень Ферми обозначен вертикальной штриховой
линией. Обозначения те же, что и на рис. 3.3.
). Уровень Ферми обозначен вертикальной штриховой
линией. Обозначения те же, что и на рис. 3.3.
|
В таблице 3.2 приведены заселенности различных
орбиталей для
различных конфигураций. Легко заметить, что получившаяся заселенность
отличается от формальной ``химической'', и соответствует не шести, а ближе к
семи электронам в d оболочке. Причина этого в сильной гибридизации пустых
eg орбиталей с
кислородными 2p орбиталями. В НС основном
состоянии каждая eg
орбиталь, которая формально пуста, имеет
заселенность 0.33, что дает 1.3 дополнительных электрона сверх формальной
конфигурации d6. В случае
ПС состояния имеется частично
заполненная  зона с полным числом
eg электронов,
увеличенным
на 0.85 по сравнению с НС состоянием. В то же время число
t2g электронов оказалось
на 0.92 меньше, чем в НС состоянии.
Полное же число d электронов в результате осталось практически
неизменным. Потому в таблице 3.2 использовалось
обозначение
зона с полным числом
eg электронов,
увеличенным
на 0.85 по сравнению с НС состоянием. В то же время число
t2g электронов оказалось
на 0.92 меньше, чем в НС состоянии.
Полное же число d электронов в результате осталось практически
неизменным. Потому в таблице 3.2 использовалось
обозначение
 , чтобы предотвратить неверное толкование и в
соответствии с обозначениями, предложенными в [127]. Можно также
сказать, что, несмотря на формальную степень окисления
Co3+, реальная
конфигурация, например, в ПС состоянии, - смесь конфигураций
, чтобы предотвратить неверное толкование и в
соответствии с обозначениями, предложенными в [127]. Можно также
сказать, что, несмотря на формальную степень окисления
Co3+, реальная
конфигурация, например, в ПС состоянии, - смесь конфигураций
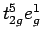 и
и
 .
.
Стоит также упомянуть некоторые другие аспекты, касающиеся вычислений. Как
видно из рис. 3.3, в случае НС конфигурации
занятые
состояния, наиболее близкие к энергии Ферми, образованы, главным образом,
кислородными состояниями
(заметим, что на рисунках 3.3-3.5
парциальные плотности состояний даны в расчете на один атом, а в
одной формульной единице содержатся три атома кислорода). Следовательно,
конечное состояние фотоэлектронного спектра для НС состояния
формально соответствует конфигурации
 . В то же время
электронные возбуждения происходят, главным образом, на
eg орбитали Co,
гибридизованные с 2p состояниями кислорода. Однако в конфигурации
ПС, которая по нашим вычислениям металлическая
(рис. 3.4),
состояния на уровне Ферми содержат сравнимые веса и
eg орбиталей Co и
2p орбиталей O.
. В то же время
электронные возбуждения происходят, главным образом, на
eg орбитали Co,
гибридизованные с 2p состояниями кислорода. Однако в конфигурации
ПС, которая по нашим вычислениям металлическая
(рис. 3.4),
состояния на уровне Ферми содержат сравнимые веса и
eg орбиталей Co и
2p орбиталей O.
Полученное ПС состояние оказалось полностью поляризованным, что
связано с полуметаллической ферромагнитной природой решения: магнитный
момент на формульную единицу 2  , то есть он соответствует спину S=1.
В этом смысле вычисления согласуются с ионной картиной, в которой
конфигурация ПС состояния Co - это
d6 (
, то есть он соответствует спину S=1.
В этом смысле вычисления согласуются с ионной картиной, в которой
конфигурация ПС состояния Co - это
d6 (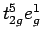 ) с S=1.
) с S=1.
Состояние ПС оказалось полуметаллическим
ферромагнетиком [140],
в котором на уровне Ферми есть только электроны с одной
проекцией спина (подзоны противоположного спина полностью заполнены).
Ферромагнитное упорядочение магнитных моментов может быть, конечно,
артефактом использованной схемы. В принципе, метод LDA+U
ориентирован на
описание локальных корреляционных эффектов, таких как образование
хаббардовских зон и локальных магнитных моментов, которые должны
существовать и в парамагнитной фазе. Однако технически в вычислениях
необходимо предполагать дальний магнитный порядок в соответствии с
трансляционной симметрией кристалла![[*]](footnote.gif) . Результаты, полученные таким способом,
показывают, есть
щель или нет, и дают оценку локального магнитного момента.
. Результаты, полученные таким способом,
показывают, есть
щель или нет, и дают оценку локального магнитного момента.
Хотя ПС состояние, согласно расчету, оказалось металлическим,
плотность состояний на уровне Ферми очень мала,
n(EF)=0.36 состояний на
эВ на одну формульную единицу. Это, возможно, показывает, что нетрудно
будет сделать это состояние полупроводящим, см. обсуждение в разделе
3.3.
Результаты, представленные выше, показывают, что первая возбужденная
конфигурация лежит всего на 0.24 эВ выше, чем основное состояние
с НС конфигурацией. Экспериментально установлено, что существует
переход из
немагнитного (НС) состояния в магнитное при увеличении
температуры. В соответствии с [125], этот переход происходит около
90 K. Так как ближайшее магнитное состояние - это состояние ПС
(ВС состояние лежит, в соответствии с нашими расчетами,
значительно выше по энергии на 0.65 эВ), нами предлагается описывать
переход LaCoO3 из
немагнитного состояния в магнитное как переход ионов
Co3+ из НС в
ПС состояние.
Рис. 3.6:
Рассчитанные полные энергии для различных спиновых состояний
LaCoO3 относительно
энергии
 состояния при 4 K в зависимости
от R
состояния при 4 K в зависимости
от R c постоянной решетки и соответствующей температуры.
c постоянной решетки и соответствующей температуры. |
Хорошо известно (см., например, [126, 128, 127, 129]), что Co в высокоспиновом
состоянии имеет больший ионный радиус, чем в низкоспиновом, и переход
НС-ВС сопровождается изменением объема. Принимая это во внимание,
были выполнены вычисления электронной структуры
LaCoO3 для различных
значений постоянной решетки, которые могут имитировать влияние температуры
(через термическое расширение). На рис. 3.6
приведены полные
энергии для различных спиновых состояний Co как функцию параметров решетки
относительно энергии
 состояния для параметра решетки,
соответствующего 4 K. На этом рисунке реальные параметры решетки,
использовавшиеся в вычислениях, показаны на горизонтальной оси вместе с
температурной шкалой (были использованы параметры решетки, включая
постоянную решетки и ромбоэдрический угол, как функцию температуры,
измеренные в [130]). Можно увидеть, что с увеличением
объема
(или с увеличением температуры) энергия ПС состояния пересекает
кривую НС состояния, что соответствует НС-ПС переходу.
По результатам вычислений это пересечение происходит при параметрах
решетки, соответствующих 150 K - немного выше, чем экспериментальное
значение около 90 K. Заметим, что ВС состояние лежит значительно
выше по энергии даже при температурах больше 600 K.
состояния для параметра решетки,
соответствующего 4 K. На этом рисунке реальные параметры решетки,
использовавшиеся в вычислениях, показаны на горизонтальной оси вместе с
температурной шкалой (были использованы параметры решетки, включая
постоянную решетки и ромбоэдрический угол, как функцию температуры,
измеренные в [130]). Можно увидеть, что с увеличением
объема
(или с увеличением температуры) энергия ПС состояния пересекает
кривую НС состояния, что соответствует НС-ПС переходу.
По результатам вычислений это пересечение происходит при параметрах
решетки, соответствующих 150 K - немного выше, чем экспериментальное
значение около 90 K. Заметим, что ВС состояние лежит значительно
выше по энергии даже при температурах больше 600 K.
Полная энергия для всех трех решений (НС, ПС и ВС)
уменьшается с увеличением объема, и минимумы достигаются только для
параметров решетки, соответствующих высокой температуре. При этом значении
объема полная энергия ПС состояния немного ниже, чем НС.
Хорошо известно, что равновесные значения объема, вычисленные с
помощью LSDA, всегда на несколько процентов меньше, чем экспериментальный
объем [28], так как LSDA переоценивает силу связи.
LDA+U, с
другой стороны, недооценивает силу связи, так как рассматривает d
состояния как локализованные. В обоих случаях вычисленные параметры решетки
существенно отличаются от экспериментальных значений. Гудинаф предположил
[126], что магнитный переход в
LaCoO3 определяется тем
фактом, что энергия кристаллического поля
 только немного
больше, чем энергия внутриатомного обмена
только немного
больше, чем энергия внутриатомного обмена
 . Энергия
кристаллического поля определяется энергией переноса 3d-2p,
что очень
сильно зависит от кристаллического объема. Поэтому, если проводить
вычисления с параметрами решетки, соответствующими вычисленному
равновесному объему, то тонкий баланс между
. Энергия
кристаллического поля определяется энергией переноса 3d-2p,
что очень
сильно зависит от кристаллического объема. Поэтому, если проводить
вычисления с параметрами решетки, соответствующими вычисленному
равновесному объему, то тонкий баланс между
 и
и
 будет нарушен. Наши результаты показывают, что для низкотемпературных
параметров решетки
будет нарушен. Наши результаты показывают, что для низкотемпературных
параметров решетки
 несколько больше
несколько больше
 , но даже
небольшое изменение объема (соответствующее изменению температуры до 150 K)
инвертирует это отношение.
, но даже
небольшое изменение объема (соответствующее изменению температуры до 150 K)
инвертирует это отношение.
Рис. 3.7:
Схематическое представление различных конфигураций Co
 в низко- (a), промежуточно- (b) и
высоко- (c) спиновых состояниях. Кружок обозначает дырку в
кислородной p оболочке.
в низко- (a), промежуточно- (b) и
высоко- (c) спиновых состояниях. Кружок обозначает дырку в
кислородной p оболочке.
|
Таким образом, на основе полученных результатов можно заключить, что
переход из немагнитного состояния в магнитное в
LaCoO3 происходит
наиболее вероятно между низкоспиновым состоянием и состоянием с
промежуточным спином, а не между низко- и высокоспиновым состояниями.
Причину стабилизации состояния с промежуточным спином можно объяснить
следующим образом. Различные конфигурации
Co3+
(d6) показаны на
рис. 3.7. Здесь
t2g и
eg - атомные d
состояния,
расщепленные кристаллическим полем (расщепление 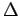 =10 Dq). В чисто
ионной картине ожидается, что в зависимости от отношения между
=10 Dq). В чисто
ионной картине ожидается, что в зависимости от отношения между 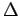 и
внутриатомного обмена J либо НС, либо ВС состояние
будет стабильным (если энергия НС состояния E
и
внутриатомного обмена J либо НС, либо ВС состояние
будет стабильным (если энергия НС состояния E берется
равной нулю, то энергия ПС состояния
берется
равной нулю, то энергия ПС состояния
 , а энергия
ВС состояния
, а энергия
ВС состояния
 , так что НС состояние
основное при
, так что НС состояние
основное при  , а ВС - при
, а ВС - при  ; состояние
ПС в этой схеме всегда будет лежать выше). Однако, как
упоминалось в разделе 3, оксиды с необычно высокой
валентностью переходных металлов имеют тенденцию к заполнению d оболочки
до заселенности, соответствующей более низкой валентности с дополнительной
дыркой, расположенной главным образом на кислороде (в данном случае
вместо конфигурации d6
получается
; состояние
ПС в этой схеме всегда будет лежать выше). Однако, как
упоминалось в разделе 3, оксиды с необычно высокой
валентностью переходных металлов имеют тенденцию к заполнению d оболочки
до заселенности, соответствующей более низкой валентности с дополнительной
дыркой, расположенной главным образом на кислороде (в данном случае
вместо конфигурации d6
получается
 ). В этом случае
d-p гибридизация особенно сильна и играет критическую роль.
Данные рассуждения также согласуются с нашим вычислениями
(см. таблицу 3.2).
). В этом случае
d-p гибридизация особенно сильна и играет критическую роль.
Данные рассуждения также согласуются с нашим вычислениями
(см. таблицу 3.2).
Особенно важна гибридизация 2p состояний кислорода с
eg орбиталями
кобальта. Можно показать, что она сильнее для ПС, чем для ВС:
в этом случае больше каналов
p-eg
гибридизации (наиболее выгодная конфигурация типа
 , примешанная к
d6, также
показана на рис. 3.7). Другими словами,
если эти конфигурации
(
, примешанная к
d6, также
показана на рис. 3.7). Другими словами,
если эти конфигурации
( ) доминируют, то состояние, соответствующее
основному состоянию d7
конфигурации, будет иметь наинизшую энергию. Известно, что
для d7
(Co2+) это в точности
конфигурация, изображенная на
рис. 3.7(b), - то есть та, которая дает
ПС
состояние. Такова возможная физическая причина, почему ПС
конфигурация может лежать ниже ВС, и может стать основным
состоянием для расширенной решетки (т.е. при более высоких температурах).
) доминируют, то состояние, соответствующее
основному состоянию d7
конфигурации, будет иметь наинизшую энергию. Известно, что
для d7
(Co2+) это в точности
конфигурация, изображенная на
рис. 3.7(b), - то есть та, которая дает
ПС
состояние. Такова возможная физическая причина, почему ПС
конфигурация может лежать ниже ВС, и может стать основным
состоянием для расширенной решетки (т.е. при более высоких температурах).
Переход из немагнитного состояния в магнитное, происходящий при 90 K,
который теперь мы связываем с переходом НС-ПС, достаточно разумно
описывается нашей моделью. Температура перехода, полученная в наших
вычислениях (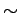 150 K), лежит не так далеко от экспериментально
наблюдаемой. В работе [125] относительное изменение параметра
решетки (
150 K), лежит не так далеко от экспериментально
наблюдаемой. В работе [125] относительное изменение параметра
решетки ( ) при этом переходе проверялось соотношением (см.
публикации [142, 143])
) при этом переходе проверялось соотношением (см.
публикации [142, 143])
 |
(3.1) |
где  - энергетическая щель (в работе [125] она
использовалась как параметр подгонки), а
- энергетическая щель (в работе [125] она
использовалась как параметр подгонки), а  - вырождение магнитного
состояния. Так как ВС состояние предполагалось основным при высокой
температуре в [125], вырождение было взято как
- вырождение магнитного
состояния. Так как ВС состояние предполагалось основным при высокой
температуре в [125], вырождение было взято как  =15
[трехкратное вырождение
t2g орбитали,
умноженное на спиновое вырождение
(2S+1) с S=2; см. рис. 3.7(c)].
В нашей интерпретации
вырождение будет
=15
[трехкратное вырождение
t2g орбитали,
умноженное на спиновое вырождение
(2S+1) с S=2; см. рис. 3.7(c)].
В нашей интерпретации
вырождение будет  =18 [трехкратное вырождение
t2g орбитали,
умноженное на двухкратное вырождение
eg на спиновое
вырождение (2S+1) с
S=1, см. рис. 3.7(b)]. Таким образом,
=18 [трехкратное вырождение
t2g орбитали,
умноженное на двухкратное вырождение
eg на спиновое
вырождение (2S+1) с
S=1, см. рис. 3.7(b)]. Таким образом,  будет с таким
же успехом удовлетворять соотношению (3.1)
при использовании
нашей интерпретации с практически тем же самым значением энергетической
щели
будет с таким
же успехом удовлетворять соотношению (3.1)
при использовании
нашей интерпретации с практически тем же самым значением энергетической
щели  .
.
Картина ПС состояния может также помочь решить еще одну проблему,
упоминавшуюся в [125]: корреляции
между магнитными узлами в
LaCoO3 не антиферромагнитные,
а (слабо) ферромагнитные. Однако между
высокоспиновыми ионами Co3+,
в которых eg оболочка наполовину
заполнена ( ), можно ожидать только антиферромагнитных корреляций. В
случае ПС Co, где ионы имеют формальную конфигурацию
), можно ожидать только антиферромагнитных корреляций. В
случае ПС Co, где ионы имеют формальную конфигурацию  ,
можно ожидать ферромагнитного обменного взаимодействия, особенно если эти
орбитали упорядочены; см. обсуждение ниже (хорошо известный пример -
K2CuF4
[1]).
,
можно ожидать ферромагнитного обменного взаимодействия, особенно если эти
орбитали упорядочены; см. обсуждение ниже (хорошо известный пример -
K2CuF4
[1]).
Возможное орбитальное упорядочение в
LaCoO3
Концепция перехода из НС в ПС состояние ионов
Co3+
довольно разумно описывает переход от немагнитного состояния к магнитному,
наблюдаемый в LaCoO3.
В то же время было установлено, что первый переход
при 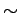 90 K оставляет это соединение полупроводящим, в то время
как вычисленное нами ПС состояние имеет металлический характер
энергетического спектра. Возможно ли преодолеть эту несогласованность?
90 K оставляет это соединение полупроводящим, в то время
как вычисленное нами ПС состояние имеет металлический характер
энергетического спектра. Возможно ли преодолеть эту несогласованность?
Как видно из рис. 3.7(b), состояние с
промежуточным спином
имеет сильное двукратное вырождение (конфигурация  ). Для
локализованных электронов это типичная ян - теллеровская ситуация. Например,
в [1] было предложено и в [90] подтверждено
вычислениями, что в KCuF3
существует особого рода орбитальный и
магнитный порядок d ионов в простой кубической решетке с одним
электроном или дыркой в двукратно вырожденном
eg уровне. Ситуация с
ПС в LaCoO3 очень
напоминает случай в KCuF3
(принимая во внимание, что в
LaCoO3 имеется ромбоэдрическое
искажение, и что там уже два иона Co на
элементарную ячейку, так что антиорбитальное упорядочение вполне
согласуется с существующими экспериментальными данными).
). Для
локализованных электронов это типичная ян - теллеровская ситуация. Например,
в [1] было предложено и в [90] подтверждено
вычислениями, что в KCuF3
существует особого рода орбитальный и
магнитный порядок d ионов в простой кубической решетке с одним
электроном или дыркой в двукратно вырожденном
eg уровне. Ситуация с
ПС в LaCoO3 очень
напоминает случай в KCuF3
(принимая во внимание, что в
LaCoO3 имеется ромбоэдрическое
искажение, и что там уже два иона Co на
элементарную ячейку, так что антиорбитальное упорядочение вполне
согласуется с существующими экспериментальными данными).
Эта возможность была проверена повторением вычислений в предположении
существования орбитального порядка. Структура соответствующего
упорядоченного состояния состояла из ферромагнитных плоскостей (001) с
антиферромагнитным упорядочением между плоскостями. Занятые
eg орбитали
предполагались меняющимися, в качестве старта были выбраны следующие
орбитали:
 и
и
 , см. рис. 3.8.
, см. рис. 3.8.
Рис. 3.8:
Спиновое и орбитальное упорядочение для занятых
eg орбиталей
в орбитально упорядоченном промежуточноспиновом состоянии. Для простоты
показана идеальная кубическая структура ионов Co. |
Чтобы представить расположение других d орбиталей на рисунке,
предположим, что ионы Co находятся в конфигурации
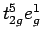 , в
которой
, в
которой
 орбиталь занята (соответствующий узел на
рис. 3.8 имеет обозначение 1). Для этого
состояния остальные
три орбитали eg пусты,
а все t2g орбитали
заполнены за исключением
орбиталь занята (соответствующий узел на
рис. 3.8 имеет обозначение 1). Для этого
состояния остальные
три орбитали eg пусты,
а все t2g орбитали
заполнены за исключением
 . Такой выбор минимизирует кулоновскую энергию
взаимодействия t2g и
eg. Для соседних ионов
Co (узел 2 на рис. 3.8)
eg электрон занимает
. Такой выбор минимизирует кулоновскую энергию
взаимодействия t2g и
eg. Для соседних ионов
Co (узел 2 на рис. 3.8)
eg электрон занимает
 орбиталь, а
t2g дырка -
орбиталь, а
t2g дырка -
 орбиталь. Вычисления были сделаны для
реальной ромбоэдрической кристаллической структуры с параметром решетки,
соответствующим 71 K. Используя это состояние в качестве стартового, были
проведены самосогласованные вычисления. Полученные плотности состояний,
соответствующие такому орбитально упорядоченному ПС состоянию,
показаны на рис. 3.9.
орбиталь. Вычисления были сделаны для
реальной ромбоэдрической кристаллической структуры с параметром решетки,
соответствующим 71 K. Используя это состояние в качестве стартового, были
проведены самосогласованные вычисления. Полученные плотности состояний,
соответствующие такому орбитально упорядоченному ПС состоянию,
показаны на рис. 3.9.
Рис. 3.9:
Полная и парциальная плотности состояний, полученные в методе
LDA+U для LaCoO3
с ионами Co в орбитально упорядоченном
промежуточноспиновом состоянии. (a) Полная плотность состояний
(на четыре формульных единицы и оба спина. (b) Парциальные плотности
eg состояний Co,
например, для узла 1 Co на рис. 3.8:
непрерывная линия обозначает
 состояния, штриховая -
состояния, штриховая -
 .
(c) то же что и (b) в окрестности Ферми уровня.
.
(c) то же что и (b) в окрестности Ферми уровня.
|
Прежде всего нужно отметить, что этот тип орбитального порядка устойчив по
отношению к процессу самосогласования, и, следовательно, существует решение
с такой симметрией![[*]](footnote.gif) . Энергетический спектр получился бесщелевым
полупроводником. Широкая зона
eg, которая пересекает
уровень Ферми в случае состояния ПС без орбитального порядка
(см. рис. 3.4), теперь расщепляется. Вершина
валентной зоны образована (для одной подрешетки, например, для узла 1 Co)
состояниями
. Энергетический спектр получился бесщелевым
полупроводником. Широкая зона
eg, которая пересекает
уровень Ферми в случае состояния ПС без орбитального порядка
(см. рис. 3.4), теперь расщепляется. Вершина
валентной зоны образована (для одной подрешетки, например, для узла 1 Co)
состояниями
 , и дно
зоны проводимости - состояниями
, и дно
зоны проводимости - состояниями
 , гибридизованными с
кислородными состояниями. Что касается состояний
t2g, то характер их
энергетического распределения практически не изменяется по сравнению со
случаем ПС состояния без орбитального порядка. Спиновый магнитный
момент Co оказался равным 1.87
, гибридизованными с
кислородными состояниями. Что касается состояний
t2g, то характер их
энергетического распределения практически не изменяется по сравнению со
случаем ПС состояния без орбитального порядка. Спиновый магнитный
момент Co оказался равным 1.87  в данном орбитально упорядоченном
ПС состоянии, и он меньше, чем в состоянии без орбитального
порядка 2.11
в данном орбитально упорядоченном
ПС состоянии, и он меньше, чем в состоянии без орбитального
порядка 2.11  ).
).
Слева: Рис. 3.10.
Спиновое и орбитальное упорядочение для пустых
eg орбиталей
в орбитально упорядоченном промежуточноспиновом состоянии. Рисунок
представляет тот же самый результат, что изображен на
рис. 3.8.
Рисунки имеют разный вид вследствие того,
что на рис. 3.8 изображена схема упорядочения
занятых
орбиталей (eg электронов),
а здесь - результат расчета для пустых
орбиталей (дырок в eg
оболочке).
Справа: Рис. 3.11.
Иное возможное спиновое и орбитальное упорядочение для пустых
eg орбиталей в
орбитально упорядоченном промежуточноспиновом состоянии.
|
При сравнении двух ПС состояний с зафиксированными спиновыми
магнитными моментами 1.87  полная энергия орбитально упорядоченного
ПС состояния оказалась на 0.11 эВ ниже. Необходимость
использования фиксированного магнитного момента связана с ограничениями
вычислительной схемы. Известно, что реальное магнитное состояние
LaCoO3
- парамагнитное (с возможным ближним спиновым или орбитальным порядком). В
то же время, как было упомянуто выше, в вычислениях необходимо
устанавливать дальний магнитный порядок (антиферромагнитный для орбитально
упорядоченного ПС состояния и ферромагнитный для состояния без
орбитального порядка). Этот дальний магнитный порядок (в дополнении к
внутриатомному обмену) влияет как на локальные магнитные моменты, так и на
полную энергию. В случае дальнего антиферромагнитного порядка величина
магнитного момента, очевидно, недооценивается по сравнению с реальным
парамагнитным состоянием; для ферромагнитного случая она переоценивается.
Таким образом, для оценки относительной стабильности отдельных фаз
сравнивались полные энергии, вычисленные при одинаковых значениях
магнитного момента. Наши вычисления показывают, что в случае одинаковых
спиновых значений ПС состояние с орбитальным порядком более
предпочтительно, чем состояние без орбитального порядка.
полная энергия орбитально упорядоченного
ПС состояния оказалась на 0.11 эВ ниже. Необходимость
использования фиксированного магнитного момента связана с ограничениями
вычислительной схемы. Известно, что реальное магнитное состояние
LaCoO3
- парамагнитное (с возможным ближним спиновым или орбитальным порядком). В
то же время, как было упомянуто выше, в вычислениях необходимо
устанавливать дальний магнитный порядок (антиферромагнитный для орбитально
упорядоченного ПС состояния и ферромагнитный для состояния без
орбитального порядка). Этот дальний магнитный порядок (в дополнении к
внутриатомному обмену) влияет как на локальные магнитные моменты, так и на
полную энергию. В случае дальнего антиферромагнитного порядка величина
магнитного момента, очевидно, недооценивается по сравнению с реальным
парамагнитным состоянием; для ферромагнитного случая она переоценивается.
Таким образом, для оценки относительной стабильности отдельных фаз
сравнивались полные энергии, вычисленные при одинаковых значениях
магнитного момента. Наши вычисления показывают, что в случае одинаковых
спиновых значений ПС состояние с орбитальным порядком более
предпочтительно, чем состояние без орбитального порядка.
Теперь первый переход из немагнитного состояния в магнитное (при
температуре около 90 K) можно интерпретировать как переход ионов Co из
НС в ПС состояние со специфическим орбитальным порядком
заполненных eg орбиталей.
Наши результаты показывают, что этот переход
происходит при температуре ниже, чем 150 K. При этом переходе на узлах Co
появляется магнитный момент, в то время как соединение остается неметаллом.
Только спиновое значение эффективного магнитного момента в случае ПС
состояния (S=1)  =2.83
=2.83  - несколько ниже
экспериментального значения 3.1
- несколько ниже
экспериментального значения 3.1  - 3.4
- 3.4  . Оно будет увеличено
орбитальным вкладом, так как, в принципе, существует нескомпенсированный
момент t2g электронов
в конфигурации
. Оно будет увеличено
орбитальным вкладом, так как, в принципе, существует нескомпенсированный
момент t2g электронов
в конфигурации
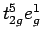 (который,
например, для ионов Co2+
обычно увеличивает значение
(который,
например, для ионов Co2+
обычно увеличивает значение  на
на
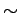 0.3
0.3  ). В работе этот эффект не был учтен численно, так как
использованная программа не включает спин - орбитальное взаимодействие.
Однако с физической точки зрения можно ожидать, что этот эффект будет иметь
место. Дополнительное изменение
). В работе этот эффект не был учтен численно, так как
использованная программа не включает спин - орбитальное взаимодействие.
Однако с физической точки зрения можно ожидать, что этот эффект будет иметь
место. Дополнительное изменение  может быть связано с очень
сильной d-p гибридизацией, которая ведет к большому вкладу
в полную волновую функцию состояния
может быть связано с очень
сильной d-p гибридизацией, которая ведет к большому вкладу
в полную волновую функцию состояния
 (
( ). В этом состоянии эффективный
момент инов Co от высокоспиновых ионов
Co2+
(S=3/2) компенсируется противоположной
поляризацией кислородной p оболочки (S=-1/2)
[заметим, что эта картина
подтверждается вычислениями (см. табл. 3.2),
где локальный спиновый момент Co 2.11
). В этом состоянии эффективный
момент инов Co от высокоспиновых ионов
Co2+
(S=3/2) компенсируется противоположной
поляризацией кислородной p оболочки (S=-1/2)
[заметим, что эта картина
подтверждается вычислениями (см. табл. 3.2),
где локальный спиновый момент Co 2.11  , а полный спиновый момент на ячейку
2
, а полный спиновый момент на ячейку
2  ]. Этот факт может существенно изменить значение
]. Этот факт может существенно изменить значение  в
экспериментах по измерению восприимчивости.
в
экспериментах по измерению восприимчивости.
Состояние ПС с формальной конфигурацией
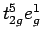 может
иметь орбитальное упорядочение из-за двукратно вырожденных
eg орбиталей
(сильная ян - теллеровская природа этого соединения). Это и получилось в
нашем случае: орбитально упорядоченное состояние может быть приближенно
описано как перемена занятых
может
иметь орбитальное упорядочение из-за двукратно вырожденных
eg орбиталей
(сильная ян - теллеровская природа этого соединения). Это и получилось в
нашем случае: орбитально упорядоченное состояние может быть приближенно
описано как перемена занятых
 и
и
 орбиталей.
орбиталей.
В соответствии с вычислениями, это упорядочение вызывает расщепление
eg
( ) зоны, приводя практически к ситуации с нулевой щелью,
и Ферми уровнем, лежащим в щели. Второй постепенный переход в металлическое
состояние (
) зоны, приводя практически к ситуации с нулевой щелью,
и Ферми уровнем, лежащим в щели. Второй постепенный переход в металлическое
состояние (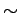 600 K) с увеличением эффективного магнитного момента до
600 K) с увеличением эффективного магнитного момента до
 =4.0
=4.0 может быть ассоциирован с исчезновением орбитального
порядка при увеличении температуры внутри ПС состояния.
ПС состояние без орбитального порядка по результатам вычислений
оказалось
металлом с большим магнитным моментом. Наши вычисления показывают, что
второй переход не имеет отношения к ВС состоянию ионов Co, потому
что ВС решение лежит выше по энергии. Кроме того, если бы
ВС реализовывалось, то, согласно расчетам, получалось бы
полупроводящее состояние вместо металлического, как это следует из
эксперимента.
может быть ассоциирован с исчезновением орбитального
порядка при увеличении температуры внутри ПС состояния.
ПС состояние без орбитального порядка по результатам вычислений
оказалось
металлом с большим магнитным моментом. Наши вычисления показывают, что
второй переход не имеет отношения к ВС состоянию ионов Co, потому
что ВС решение лежит выше по энергии. Кроме того, если бы
ВС реализовывалось, то, согласно расчетам, получалось бы
полупроводящее состояние вместо металлического, как это следует из
эксперимента.
Итак, в этом разделе были представлены результаты вычисления электронной
структуры LaCoO3 в приближении
LDA+U. При 4 K немагнитное полупроводящее
решение с ионами Co в низкоспиновом состоянии имеет наинизшую полную
энергию. Найдены также три стабильных возбужденных конфигурации (две с
промежуточным спином и одна высокоспиновая) с локальными магнитными
моментами на узлах Co. Зона Co
t2g состояний узкая,
в то время как
eg состояния образуют
широкую зону. Вследствие сильной гибридизации
между Co eg состояниями
и O 2p состояниями, что формально можно
представить как состояние иона
Co3+ в конфигурации
 , оказалось, что величины полных энергий
системы в НС и ПС состояниях близки между собой. С увеличением
параметра решетки, соответствующего термическому расширению, можно ожидать
два перехода: первый происходит от НС состояния к ПС
состоянию с орбитальным порядком, которое в наших вычислениях -
полупроводник с нулевой щелью. Второй переход происходит внутри ПС
состояния ионов Co3+ и связан
с постепенным разупорядочением
занятых eg орбиталей.
, оказалось, что величины полных энергий
системы в НС и ПС состояниях близки между собой. С увеличением
параметра решетки, соответствующего термическому расширению, можно ожидать
два перехода: первый происходит от НС состояния к ПС
состоянию с орбитальным порядком, которое в наших вычислениях -
полупроводник с нулевой щелью. Второй переход происходит внутри ПС
состояния ионов Co3+ и связан
с постепенным разупорядочением
занятых eg орбиталей.
Концепция фазовых переходов в
LaCoO3, связанная, главным
образом, с
промежуточноспиновым состоянием, является хорошим кандидатом для объяснения
необычных свойств как этого соединения, так и других оксидных соединений
кобальта. За время, прошедшее после опубликования представляемых
результатов в журнале ``Physical Review B'' [13], данная
концепция использовалась во многих работах различных авторов и даже вошла в
обзор [144]. Совсем недавно появилось первое
экспериментальное
доказательство реализации ПС состояния в
LaCoO3 [145]. В этой работе были проведены измерения
магнитной восприимчивости
и исследования температурного расширения монокристалла
LaCoO3 и
предпринята попытка теоретического воспроизведения всех полученных
зависимостей в рамках четырех возможных сценариев переходов ионов Co в
различные спиновые состояния: НС
 ПС,
НС
ПС,
НС
 ВС, с орбитальным порядком и без него.
Полученные данные могли быть описаны только в терминах перехода иона
Co3+ с ростом температуры
из НС основного состояния
ВС, с орбитальным порядком и без него.
Полученные данные могли быть описаны только в терминах перехода иона
Co3+ с ростом температуры
из НС основного состояния
 в ПС состояние
в ПС состояние
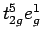 без (100-500 K) и
с (>500 K) eg
орбитальным вырождением. Такой результат полностью
совпадает со сценарием, предложенным в этой главе.
без (100-500 K) и
с (>500 K) eg
орбитальным вырождением. Такой результат полностью
совпадает со сценарием, предложенным в этой главе.
Сноски:
- ...
состояние
![[*]](footnote.gif)
- Соответствующие одноэлектронные конфигурации d
оболочки иона Co3+ -
 для НС состояния и
для НС состояния и
 для ВС состояния.
для ВС состояния.
- ...
энергии
![[*]](footnote.gif)
- В ионной картине еще одно возможное -
промежуточноспиновое состояние иона
Co3+ с конфигурацией
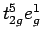 - никогда не может быть основным, поскольку
ожидается, что
оно должно лежать по крайней мере на 1 эВ выше, чем НС или
ВС состояния.
- никогда не может быть основным, поскольку
ожидается, что
оно должно лежать по крайней мере на 1 эВ выше, чем НС или
ВС состояния.
- ... кристалла
![[*]](footnote.gif)
- Сравнительно недавно
появилась экспериментальная работа
[141] по измерению
температурной зависимости магнитной восприимчивости однофазных порошков
LaCoO3. Результаты
свидетельствуют о существовании двух типов
ферромагнитного и антиферромагнитного взаимодействий в
LaCoO3 при низких
температурах.
- ... симметрией
![[*]](footnote.gif)
- Как показали наши последние расчеты, имевшие
целью воспроизвести излагаемые результаты в рамках современной расчетной
схемы, существует и другое стабильное орбитальное упорядочение
eg
электронов (дырок); см. рис. 3.10,
3.11.
Следующая страница:
Глава 4.
``CrO2 - самолегированный
ферромагнетик с механизмом двойного обмена''
Предыдущая страница:
Глава 2. ``Исследование причин упорядочения занятых
eg орбиталей ионов
Mn3+ в манганитах
Pr1-xCaxMnO3
(x=0 и
x=1/2) и
La7/8Sr1/8MnO3''
Вернуться к содержанию диссертации
![[*]](footnote.gif) . Переход полупроводник - металл
происходит в диапазоне температур 400-600 K - значительно выше магнитного
перехода. Природу того, что
. Переход полупроводник - металл
происходит в диапазоне температур 400-600 K - значительно выше магнитного
перехода. Природу того, что
![]() 90 K
происходит переход от немагнитного к парамагнитному полупроводнику, а при
90 K
происходит переход от немагнитного к парамагнитному полупроводнику, а при
![]() 500 K наблюдается переход полупроводник - металл.
Несмотря на то, что
большое количество исследований было проведено с начала 1960-х годов,
характер перехода и природа температурной зависимости спинового состояния
до сих пор не ясны. Например, температурная зависимость магнитной
восприимчивости имеет пик около 90 K, после которого при повышении
температуры следует спад магнитной восприимчивости по закону
Кюри - Вейсса [125], что интерпретировалось как переход ионов
500 K наблюдается переход полупроводник - металл.
Несмотря на то, что
большое количество исследований было проведено с начала 1960-х годов,
характер перехода и природа температурной зависимости спинового состояния
до сих пор не ясны. Например, температурная зависимость магнитной
восприимчивости имеет пик около 90 K, после которого при повышении
температуры следует спад магнитной восприимчивости по закону
Кюри - Вейсса [125], что интерпретировалось как переход ионов
![[*]](footnote.gif) . Переход полупроводник - металл
происходит в диапазоне температур 400-600 K - значительно выше магнитного
перехода. Природу того, что
. Переход полупроводник - металл
происходит в диапазоне температур 400-600 K - значительно выше магнитного
перехода. Природу того, что

![]() только незначительно больше, чем энергия внутриатомного обмена
только незначительно больше, чем энергия внутриатомного обмена
![]() (рис. 3.1). В
такой модели основное
состояние ионов Co - НС (
(рис. 3.1). В
такой модели основное
состояние ионов Co - НС (![]() ,
, ![]() ,
, ![[*]](footnote.gif) . Увеличение температуры приводит к заполнению
ВС состояния, что и отражается в измерениях магнитной
восприимчивости. Переход полупроводник - металл интерпретировался
качественно как образование широкой
. Увеличение температуры приводит к заполнению
ВС состояния, что и отражается в измерениях магнитной
восприимчивости. Переход полупроводник - металл интерпретировался
качественно как образование широкой ![]() зоны из локализованных
ионных
зоны из локализованных
ионных ![]() . Реальным
доказательством правильности одноэлектронного приближения было бы
отсутствие сателлитов в фотоэмиссионном спектре. Также фотоэмиссионные
спектры, с которыми проводилось сравнение в [56], были получены
при комнатной температуре, при которой
. Реальным
доказательством правильности одноэлектронного приближения было бы
отсутствие сателлитов в фотоэмиссионном спектре. Также фотоэмиссионные
спектры, с которыми проводилось сравнение в [56], были получены
при комнатной температуре, при которой
![]() ). Из-за сильной ян - теллеровской природы этой
конфигурации в этом состоянии может произойти орбитальное упорядочение.
Состояние с орбитальным порядком в наших вычислениях оказалось
неметаллическим (в действительности полупроводник с практически нулевой
щелью). С дальнейшим увеличением температуры орбитальное упорядочение может
постепенно разрушаться, что может объяснить переход в металлическое
состояние в
). Из-за сильной ян - теллеровской природы этой
конфигурации в этом состоянии может произойти орбитальное упорядочение.
Состояние с орбитальным порядком в наших вычислениях оказалось
неметаллическим (в действительности полупроводник с практически нулевой
щелью). С дальнейшим увеличением температуры орбитальное упорядочение может
постепенно разрушаться, что может объяснить переход в металлическое
состояние в 
![]() : заселенности орбиталей xy, yz и
zx примерно одинаковы
для НС конфигурации, также как и заселенности орбиталей
: заселенности орбиталей xy, yz и
zx примерно одинаковы
для НС конфигурации, также как и заселенности орбиталей
![]() ). Начальная спиновая поляризация
исчезает в процессе самосогласования, что в результате приводит к
немагнитному решению. Спектр зарядовых возбуждений имеет полупроводниковый
характер в соответствии с экспериментальными данными [138] (и
в противоположность результату LDA [132]) со щелью, равной
2.06 эВ. Вершина валентной зоны
(рис. 3.3) состоит из смеси 2p
кислородных состояний и
). Начальная спиновая поляризация
исчезает в процессе самосогласования, что в результате приводит к
немагнитному решению. Спектр зарядовых возбуждений имеет полупроводниковый
характер в соответствии с экспериментальными данными [138] (и
в противоположность результату LDA [132]) со щелью, равной
2.06 эВ. Вершина валентной зоны
(рис. 3.3) состоит из смеси 2p
кислородных состояний и

![]() 0.3 эВ. Оптические измерения [139]
дают
0.3 эВ. Оптические измерения [139]
дают ![]() эВ. Большее значение щели, полученное из вычислений,
может быть объяснено хорошо известным фактом, что приближение среднего
поля, которое является основой метода
эВ. Большее значение щели, полученное из вычислений,
может быть объяснено хорошо известным фактом, что приближение среднего
поля, которое является основой метода ![]() с максимальным значением спина
с максимальным значением спина
![]() =4
=4 ![]() ). Это соответствует чисто ионной
модели, а гибридизация 3d орбиталей Co с кислородными 2p
орбиталями и
образование зон в твердом теле могут значительно изменить это ионное
значение. Такая ренормализация была получена в наших вычислениях
(таблица 3.2).
Начальная конфигурация
). Это соответствует чисто ионной
модели, а гибридизация 3d орбиталей Co с кислородными 2p
орбиталями и
образование зон в твердом теле могут значительно изменить это ионное
значение. Такая ренормализация была получена в наших вычислениях
(таблица 3.2).
Начальная конфигурация
![]() (две
дырки на орбиталях
(две
дырки на орбиталях
![]() ,
,
![]() из
из
![]() ,
,
![]() из
набора
из
набора ![]() =3.16
=3.16 ![]() . Полная энергия этого ВС решения на
0.65 эВ (в расчете на одну формульную единицу) выше, чем НС
конфигурация
. Полная энергия этого ВС решения на
0.65 эВ (в расчете на одну формульную единицу) выше, чем НС
конфигурация
![]() основного состояния. Оказалось, что существует
решение с промежуточным спином
(вторая строчка в таблице 3.2,
значение магнитного момента
основного состояния. Оказалось, что существует
решение с промежуточным спином
(вторая строчка в таблице 3.2,
значение магнитного момента
![]() =2.11
=2.11 ![]() ),
которое ниже по полной энергии, чем ВС решение (0.24 эВ в расчете
на одну формульную единицу относительно основного состояния НС).
Это решение было получено, когда старт процесса самосогласования происходил
из начальной конфигурации
),
которое ниже по полной энергии, чем ВС решение (0.24 эВ в расчете
на одну формульную единицу относительно основного состояния НС).
Это решение было получено, когда старт процесса самосогласования происходил
из начальной конфигурации
![]() , когда только один электрон был
перенесен из
, когда только один электрон был
перенесен из ![]() с частично
заполненной
с частично
заполненной ![]() зоной (
зоной (![]() ) с заселенностями
) с заселенностями
![]() и
и
![]() , равными 0.84. На языке
конфигурационного взаимодействия, используемого в кластерных расчетах, это
можно сравнить с состоянием
, равными 0.84. На языке
конфигурационного взаимодействия, используемого в кластерных расчетах, это
можно сравнить с состоянием
![]() , где
, где
![]() обозначает дырку в 2p состояниях кислорода.
обозначает дырку в 2p состояниях кислорода.
![]() зона, образуемая
зона, образуемая
![]() орбиталями,
очень широкая, и расщепление зон недостаточно сильно, чтобы образовать
энергетическую щель в случае ПС состояния. Щель между полностью
заполненной
орбиталями,
очень широкая, и расщепление зон недостаточно сильно, чтобы образовать
энергетическую щель в случае ПС состояния. Щель между полностью
заполненной
![]() и полностью пустой
и полностью пустой
![]() зонами
появляется в ВС состоянии.
зонами
появляется в ВС состоянии.


![]() зона с полным числом
зона с полным числом
![]() , чтобы предотвратить неверное толкование и в
соответствии с обозначениями, предложенными в [127]. Можно также
сказать, что, несмотря на формальную степень окисления
, чтобы предотвратить неверное толкование и в
соответствии с обозначениями, предложенными в [127]. Можно также
сказать, что, несмотря на формальную степень окисления
![]() и
и
![]() .
.
![]() . В то же время
электронные возбуждения происходят, главным образом, на
. В то же время
электронные возбуждения происходят, главным образом, на
![]() , то есть он соответствует спину
, то есть он соответствует спину ![]() ) с
) с ![[*]](footnote.gif) . Результаты, полученные таким способом,
показывают, есть
щель или нет, и дают оценку локального магнитного момента.
. Результаты, полученные таким способом,
показывают, есть
щель или нет, и дают оценку локального магнитного момента.

![]() состояния для параметра решетки,
соответствующего 4 K. На этом рисунке реальные параметры решетки,
использовавшиеся в вычислениях, показаны на горизонтальной оси вместе с
температурной шкалой (были использованы параметры решетки, включая
постоянную решетки и ромбоэдрический угол, как функцию температуры,
измеренные в [130]). Можно увидеть, что с увеличением
объема
(или с увеличением температуры) энергия ПС состояния пересекает
кривую НС состояния, что соответствует НС-ПС переходу.
По результатам вычислений это пересечение происходит при параметрах
решетки, соответствующих 150 K - немного выше, чем экспериментальное
значение около 90 K. Заметим, что ВС состояние лежит значительно
выше по энергии даже при температурах больше 600 K.
состояния для параметра решетки,
соответствующего 4 K. На этом рисунке реальные параметры решетки,
использовавшиеся в вычислениях, показаны на горизонтальной оси вместе с
температурной шкалой (были использованы параметры решетки, включая
постоянную решетки и ромбоэдрический угол, как функцию температуры,
измеренные в [130]). Можно увидеть, что с увеличением
объема
(или с увеличением температуры) энергия ПС состояния пересекает
кривую НС состояния, что соответствует НС-ПС переходу.
По результатам вычислений это пересечение происходит при параметрах
решетки, соответствующих 150 K - немного выше, чем экспериментальное
значение около 90 K. Заметим, что ВС состояние лежит значительно
выше по энергии даже при температурах больше 600 K.
![]() только немного
больше, чем энергия внутриатомного обмена
только немного
больше, чем энергия внутриатомного обмена
![]() . Энергия
кристаллического поля определяется энергией переноса 3d-2p,
что очень
сильно зависит от кристаллического объема. Поэтому, если проводить
вычисления с параметрами решетки, соответствующими вычисленному
равновесному объему, то тонкий баланс между
. Энергия
кристаллического поля определяется энергией переноса 3d-2p,
что очень
сильно зависит от кристаллического объема. Поэтому, если проводить
вычисления с параметрами решетки, соответствующими вычисленному
равновесному объему, то тонкий баланс между
![]() и
и
![]() будет нарушен. Наши результаты показывают, что для низкотемпературных
параметров решетки
будет нарушен. Наши результаты показывают, что для низкотемпературных
параметров решетки
![]() несколько больше
несколько больше
![]() , но даже
небольшое изменение объема (соответствующее изменению температуры до 150 K)
инвертирует это отношение.
, но даже
небольшое изменение объема (соответствующее изменению температуры до 150 K)
инвертирует это отношение.

![]() =10 Dq). В чисто
ионной картине ожидается, что в зависимости от отношения между
=10 Dq). В чисто
ионной картине ожидается, что в зависимости от отношения между ![]() и
внутриатомного обмена J либо НС, либо ВС состояние
будет стабильным (если энергия НС состояния E
и
внутриатомного обмена J либо НС, либо ВС состояние
будет стабильным (если энергия НС состояния E![]() берется
равной нулю, то энергия ПС состояния
берется
равной нулю, то энергия ПС состояния
![]() , а энергия
ВС состояния
, а энергия
ВС состояния
![]() , так что НС состояние
основное при
, так что НС состояние
основное при ![]() , а ВС - при
, а ВС - при ![]() ; состояние
ПС в этой схеме всегда будет лежать выше). Однако, как
упоминалось в разделе 3, оксиды с необычно высокой
валентностью переходных металлов имеют тенденцию к заполнению d оболочки
до заселенности, соответствующей более низкой валентности с дополнительной
дыркой, расположенной главным образом на кислороде (в данном случае
вместо конфигурации
; состояние
ПС в этой схеме всегда будет лежать выше). Однако, как
упоминалось в разделе 3, оксиды с необычно высокой
валентностью переходных металлов имеют тенденцию к заполнению d оболочки
до заселенности, соответствующей более низкой валентности с дополнительной
дыркой, расположенной главным образом на кислороде (в данном случае
вместо конфигурации ![]() ). В этом случае
d-p гибридизация особенно сильна и играет критическую роль.
Данные рассуждения также согласуются с нашим вычислениями
(см. таблицу 3.2).
). В этом случае
d-p гибридизация особенно сильна и играет критическую роль.
Данные рассуждения также согласуются с нашим вычислениями
(см. таблицу 3.2).
![]() , примешанная к
, примешанная к
![]() ) доминируют, то состояние, соответствующее
основному состоянию
) доминируют, то состояние, соответствующее
основному состоянию ![]() 150 K), лежит не так далеко от экспериментально
наблюдаемой. В работе [125] относительное изменение параметра
решетки
150 K), лежит не так далеко от экспериментально
наблюдаемой. В работе [125] относительное изменение параметра
решетки ![]() )
)![]() ), можно ожидать только антиферромагнитных корреляций. В
случае ПС Co, где ионы имеют формальную конфигурацию
), можно ожидать только антиферромагнитных корреляций. В
случае ПС Co, где ионы имеют формальную конфигурацию ![]() ,
можно ожидать ферромагнитного обменного взаимодействия, особенно если эти
орбитали упорядочены; см. обсуждение ниже (хорошо известный пример -
,
можно ожидать ферромагнитного обменного взаимодействия, особенно если эти
орбитали упорядочены; см. обсуждение ниже (хорошо известный пример -
![]() 90 K оставляет это соединение полупроводящим, в то время
как вычисленное нами ПС состояние имеет металлический характер
энергетического спектра. Возможно ли преодолеть эту несогласованность?
90 K оставляет это соединение полупроводящим, в то время
как вычисленное нами ПС состояние имеет металлический характер
энергетического спектра. Возможно ли преодолеть эту несогласованность?
![]() ). Для
локализованных электронов это типичная ян - теллеровская ситуация. Например,
в [1] было предложено и в [90] подтверждено
вычислениями, что в
). Для
локализованных электронов это типичная ян - теллеровская ситуация. Например,
в [1] было предложено и в [90] подтверждено
вычислениями, что в ![]() и
и
![]() , см. рис. 3.8.
, см. рис. 3.8.

![]() , в
которой
, в
которой
![]() орбиталь занята (соответствующий узел на
рис. 3.8 имеет обозначение 1). Для этого
состояния остальные
три орбитали
орбиталь занята (соответствующий узел на
рис. 3.8 имеет обозначение 1). Для этого
состояния остальные
три орбитали ![]() . Такой выбор минимизирует кулоновскую энергию
взаимодействия
. Такой выбор минимизирует кулоновскую энергию
взаимодействия ![]() орбиталь, а
орбиталь, а
![]() орбиталь. Вычисления были сделаны для
реальной ромбоэдрической кристаллической структуры с параметром решетки,
соответствующим 71 K. Используя это состояние в качестве стартового, были
проведены самосогласованные вычисления. Полученные плотности состояний,
соответствующие такому орбитально упорядоченному ПС состоянию,
показаны на рис. 3.9.
орбиталь. Вычисления были сделаны для
реальной ромбоэдрической кристаллической структуры с параметром решетки,
соответствующим 71 K. Используя это состояние в качестве стартового, были
проведены самосогласованные вычисления. Полученные плотности состояний,
соответствующие такому орбитально упорядоченному ПС состоянию,
показаны на рис. 3.9.

![[*]](footnote.gif) . Энергетический спектр получился бесщелевым
полупроводником. Широкая зона
. Энергетический спектр получился бесщелевым
полупроводником. Широкая зона
![]() , и дно
зоны проводимости - состояниями
, и дно
зоны проводимости - состояниями
![]() , гибридизованными с
кислородными состояниями. Что касается состояний
, гибридизованными с
кислородными состояниями. Что касается состояний
![]() в данном орбитально упорядоченном
ПС состоянии, и он меньше, чем в состоянии без орбитального
порядка 2.11
в данном орбитально упорядоченном
ПС состоянии, и он меньше, чем в состоянии без орбитального
порядка 2.11 ![]() ).
).


![]() полная энергия орбитально упорядоченного
ПС состояния оказалась на 0.11 эВ ниже. Необходимость
использования фиксированного магнитного момента связана с ограничениями
вычислительной схемы. Известно, что реальное магнитное состояние
полная энергия орбитально упорядоченного
ПС состояния оказалась на 0.11 эВ ниже. Необходимость
использования фиксированного магнитного момента связана с ограничениями
вычислительной схемы. Известно, что реальное магнитное состояние
![]() =2.83
=2.83 ![]() - несколько ниже
экспериментального значения 3.1
- несколько ниже
экспериментального значения 3.1 ![]() - 3.4
- 3.4 ![]() . Оно будет увеличено
орбитальным вкладом, так как, в принципе, существует нескомпенсированный
момент
. Оно будет увеличено
орбитальным вкладом, так как, в принципе, существует нескомпенсированный
момент ![]() (который,
например, для ионов
(который,
например, для ионов ![]() на
на
![]() 0.3
0.3 ![]() ). В работе этот эффект не был учтен численно, так как
использованная программа не включает спин - орбитальное взаимодействие.
Однако с физической точки зрения можно ожидать, что этот эффект будет иметь
место. Дополнительное изменение
). В работе этот эффект не был учтен численно, так как
использованная программа не включает спин - орбитальное взаимодействие.
Однако с физической точки зрения можно ожидать, что этот эффект будет иметь
место. Дополнительное изменение ![]() может быть связано с очень
сильной d-p гибридизацией, которая ведет к большому вкладу
в полную волновую функцию состояния
может быть связано с очень
сильной d-p гибридизацией, которая ведет к большому вкладу
в полную волновую функцию состояния
![]()
![]() ).
).![]() , а полный спиновый момент на ячейку
2
, а полный спиновый момент на ячейку
2 ![]() ]. Этот факт может существенно изменить значение
]. Этот факт может существенно изменить значение ![]() в
экспериментах по измерению восприимчивости.
в
экспериментах по измерению восприимчивости.
![]() может
иметь орбитальное упорядочение из-за двукратно вырожденных
может
иметь орбитальное упорядочение из-за двукратно вырожденных
![]() и
и
![]() орбиталей.
орбиталей.
![]() ) зоны, приводя практически к ситуации с нулевой щелью,
и Ферми уровнем, лежащим в щели. Второй постепенный переход в металлическое
состояние (
) зоны, приводя практически к ситуации с нулевой щелью,
и Ферми уровнем, лежащим в щели. Второй постепенный переход в металлическое
состояние (![]() 600 K) с увеличением эффективного магнитного момента до
600 K) с увеличением эффективного магнитного момента до
![]() =4.0
=4.0![]() может быть ассоциирован с исчезновением орбитального
порядка при увеличении температуры внутри ПС состояния.
ПС состояние без орбитального порядка по результатам вычислений
оказалось
металлом с большим магнитным моментом. Наши вычисления показывают, что
второй переход не имеет отношения к ВС состоянию ионов Co, потому
что ВС решение лежит выше по энергии. Кроме того, если бы
ВС реализовывалось, то, согласно расчетам, получалось бы
полупроводящее состояние вместо металлического, как это следует из
эксперимента.
может быть ассоциирован с исчезновением орбитального
порядка при увеличении температуры внутри ПС состояния.
ПС состояние без орбитального порядка по результатам вычислений
оказалось
металлом с большим магнитным моментом. Наши вычисления показывают, что
второй переход не имеет отношения к ВС состоянию ионов Co, потому
что ВС решение лежит выше по энергии. Кроме того, если бы
ВС реализовывалось, то, согласно расчетам, получалось бы
полупроводящее состояние вместо металлического, как это следует из
эксперимента.
![]() , оказалось, что величины полных энергий
системы в НС и ПС состояниях близки между собой. С увеличением
параметра решетки, соответствующего термическому расширению, можно ожидать
два перехода: первый происходит от НС состояния к ПС
состоянию с орбитальным порядком, которое в наших вычислениях -
полупроводник с нулевой щелью. Второй переход происходит внутри ПС
состояния ионов
, оказалось, что величины полных энергий
системы в НС и ПС состояниях близки между собой. С увеличением
параметра решетки, соответствующего термическому расширению, можно ожидать
два перехода: первый происходит от НС состояния к ПС
состоянию с орбитальным порядком, которое в наших вычислениях -
полупроводник с нулевой щелью. Второй переход происходит внутри ПС
состояния ионов ![]() ПС,
НС
ПС,
НС
![]() ВС, с орбитальным порядком и без него.
Полученные данные могли быть описаны только в терминах перехода иона
ВС, с орбитальным порядком и без него.
Полученные данные могли быть описаны только в терминах перехода иона
![]() в ПС состояние
в ПС состояние
![]() без (100-500 K) и
с (>500 K)
без (100-500 K) и
с (>500 K) ![[*]](footnote.gif)
![[*]](footnote.gif)
![[*]](footnote.gif)
![[*]](footnote.gif)