Следующая страница: Глава 6.
``Магнитные свойства Ca(Mg)VnO2n+1''
Предыдущая страница: Глава 4.
``CrO2 - самолегированный
ферромагнетик с механизмом двойного обмена''
Вернуться к содержанию диссертации
Параграфы:
Глава 5. Изменение орбитальной симметрии локализованного
3d1 электрона иона
V4+ при переходе
металл - изолятор в VO2
Переход металл - изолятор в VO2
наблюдается при температуре 340 K и
сопровождается структурным переходом из немагнитной высокотемпературной
тетрагональной R фазы рутила в также немагнитную моноклинную фазу
M1.
Фаза рутила содержит цепочки вдоль направления [001] равноудаленных друг от
друга атомов ванадия. В фазе M1
по сравнению с рутилом элементарная
ячейка удваивается, все атомы ванадия слегка отклоняются от направления
[001]R, образуя зигзаги, и перестают быть
равноудаленными друг от друга, формируя пары.
Непротиворечивое теоретическое описание перехода металл - изолятор в диоксиде
ванадия до сих пор отсутствует. Возникновение неметаллического состояния
объясняется в настоящее время с двух позиций.
Если отталкиваться от результатов зонных расчетов в приближении локальной
плотности, то фазу M1
можно рассматривать как обычный зонный изолятор Пайерлса [230, 231]. Согласно другой точки
зрения, нельзя пренебрегать межэлектронными корреляциями в d оболочке
ванадия или учитывать их в среднем, как это делается в зонных расчетах.
Четверть века назад была экспериментально обнаружена еще одна изоляторная
фаза M2 с локальными магнитными моментами на
части ионов ванадия. Фаза
M2 возникает при незначительном легировании
VO2 хромом
(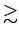 0.1 ат.%) [232] или при небольшом
напряжении вдоль оси [001]R [233] (рис. 5.1). В фазе
M2 вдоль направления
[001]R одна цепочка атомов ванадия образует
пары, как в M1 (только без отклонения от
направления [001]R), а в
соседней цепочке атомы ванадия вновь становятся равноудаленными друг от
друга, как в R фазе, но с сохранением зигзагов, как в
M1 фазе
(рис. 5.2).
0.1 ат.%) [232] или при небольшом
напряжении вдоль оси [001]R [233] (рис. 5.1). В фазе
M2 вдоль направления
[001]R одна цепочка атомов ванадия образует
пары, как в M1 (только без отклонения от
направления [001]R), а в
соседней цепочке атомы ванадия вновь становятся равноудаленными друг от
друга, как в R фазе, но с сохранением зигзагов, как в
M1 фазе
(рис. 5.2).
Рис. 5.1:
Слева: фазовая диаграмма для
V1-xCrxO2.
Рисунок воспроизведен из [232].
Справа: фазовая диаграмма
температура-напряжение для VO2.
Рисунок воспроизведен из
[233].
|
|
Рис. 5.2:
Схема взаимного положения атомов V в трех фазах
VO2. Малыми черными точками
указаны положения атомов V в R фазе,
белыми кружками - в M1 фазе, черными кружками -
в M2 фазе.
Рисунок воспроизведен из [232].
|
|
Из-за существования цепочки равноудаленных ионов
V4+ описание
изоляторного состояния фазы M2 на зонном языке
становится невозможным:
эти цепочки являются магнитными (мотт - хаббардовскими) изоляторами. Поэтому
были созданы теоретические модели, рассматривающие фазы
M1 и M2 как
мотт-хаббардовские изоляторы, исключая действия внутриатомных хаббардовских
корреляций в R фазе [234]. В то же время в литературе
приводились аргументы и экспериментальные свидетельства того, что все
структурные модификации VO2
должны рассматриваться как изоляторы Мотта - Хаббарда, а не зонные [235, 233, 236, 237, 238, 239, 144].
Обсуждение природы изоляторного состояния
VO2 продолжается на основе
новых экспериментальных и теоретических данных об электронной структуре
R
и M1 фаз. Из сравнения результатов
спектроскопических измерений и зонных
расчетов в работе [240] был сделан вывод о
том, что электронная
структура VO2 хорошо
описывается в приближении локальной плотности без
какого-либо учета корреляционных эффектов. Эксперименты по измерению
температурной зависимости скорости звука поверхностных акустических волн на
монокристалле VO2 вблизи
перехода металл - изолятор привели к заключению,
что электронные корреляции вряд ли являются движущей силой перехода
металл - изолятор [241]. На основе
двухпараметрической модели
фазового перехода металл - полупроводник пайерловского типа в работе [242] построена теория, объясняющая
структурные изменения и
образование запрещенной зоны в электронном спектре при фазовом переходе в
диоксиде ванадия. Тот же автор [243] построил теорию фазового
перехода металл - полупроводник пайерловского типа с учетом кубичного
ангармонизма межатомного взаимодействия и несфиричности атомных волновых
функций электронных квантовых состояний, при перекрытии которых образуется
квазиодномерная пайерлсовская зона в электронном спектре диоксида ванадия.
Однако исследователи электронной структуры
VO2 из ``первых принципов''
признают, что расхождение в их предсказаниях металличности моноклинной фазы
вместо экспериментально наблюдаемого ее полупроводникового характера
происходит вследствие неверного учета корреляционных эффектов в рамках
функционала плотности [244]. Измерения времени задержки в
структурах металл/оксид/металл на основе
VO2 и исследование влияния
инжекции носителей на переключение и переход металл - изолятор на планарных
переключающих устройствах [245] подтверждают исключительно
электронный мотт - хаббардовский механизм перехода в
VO2. С помощью
техники функции распределения коэрцитивных температур в работе [246] показано, что в оптических экспериментах термический фазовый
переход металл - полупроводник в диоксиде ванадия проявляет себя как
электронный переход Мотта.
Как известно, обычные зонные расчеты описывают лишь тенденцию к образованию
энергетической щели в M1 фазе
VO2 [231], давая в
результате металлический спектр в противоречие с экспериментом. Были
предприняты попытки снять это противоречие в рамках зонного подхода. Так
включение в рассмотрение электрон-фононного взаимодействия в комбинацию
модели трехмерной периодической оболочки и X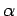 кластерного метода
дискретного варьирования привело к появлению щели в зонном спектре [247]. Введение поправки на самодействие
в рамках модельной GW
схемы также удовлетворительно воспроизвело экспериментальные свойства
неметаллической M1 фазы
VO2 [248]. Хотелось бы
отметить, что теоретические расчеты электронной структуры изоляторной фазы
M2 в настоящее время отсутствуют.
кластерного метода
дискретного варьирования привело к появлению щели в зонном спектре [247]. Введение поправки на самодействие
в рамках модельной GW
схемы также удовлетворительно воспроизвело экспериментальные свойства
неметаллической M1 фазы
VO2 [248]. Хотелось бы
отметить, что теоретические расчеты электронной структуры изоляторной фазы
M2 в настоящее время отсутствуют.
В данной главе мы попытались детально проанализировать электронную
структуру R, M1 и
M2 фаз
VO2
(для фазы M2 - впервые), в
каждом случае обращая внимание на орбиталь, заполняемую единственным
электроном иона V4+.
Для достижения этой цели мы использовали
первопринципный расчетный метод линеаризованных МТ орбиталей в приближении
сильной связи (TB LMTO) [162, 163]. Немагнитные расчеты
проводились в рамках общепринятого формализма функционала локальной
плотности LDA. В магнитных расчетах межэлектронные корреляции учитывались в
подходе LSDA+U. Использовались экспериментально
определенные параметры кристаллической решетки, взятые из литературы (R
фаза - [249],
M1 фаза - [250],
M2 фаза - [232]). При проведении расчетов
радиусы
атомных сфер V и O выбирались одинаковыми с перекрыванием в 16%, вводились
пустые сферы для заполнения объема атомных сфер до объема элементарной
ячейки, базисными функциями являлись 4s, 4p, 3d для ванадия,
3s, 2p, 3d для кислорода и 1s, 2p, 3d
для пустых сфер. В рамках
формализма функционала локальной спиновой плотности LSDA нами были
вычислены величины кулоновского U и обменного J взаимодействий в
d оболочке ванадия, причем величина U рассчитывалась с учетом
экранировки
t2g электронов
eg электронами [95]. Полученные величины
U=3.8 эВ и J=1.0 эВ были использованы
неизменными в расчетах
электронной структуры всех фаз![[*]](footnote.gif) . Таким образом,
проведенные расчеты не содержат подгоночных параметров и в этом смысле
являются первопринципными.
. Таким образом,
проведенные расчеты не содержат подгоночных параметров и в этом смысле
являются первопринципными.
Рис. 5.3:
Кристаллическая структура R фазы
VO2. Атомы
ванадия изображены большими шарами, атомы кислорода - малыми. Оси
кристаллографической системы координат обозначены большими буквами,
локальных систем координат для атомов ванадия в вершинах и в центре решетки
- малыми.
|
|
Элементарная ячейка высокотемпературной R фазы
VO2 (пространственная
группа P42/mnm) состоит из двух формульных
единиц. Атомы ванадия
образуют объемоцентрированную тетрагональную решетку и окружены
слабодеформированными кислородными октаэдрами. В таком октаэдре расстояния
V-O в направлении, перпендикулярном тетрагональной оси c, слегка больше
расстояний V-O в плоскости, параллельной c
(рис. 5.3 и таб.
5.1). В этой же плоскости углы O-V-O составляют
84.2o и 95.8o, а остальные
углы O-V-O равны 90o. Октаэдры,
окружающие атомы ванадия в вершинах и в центре решетки, развернуты на
90o вокруг c. В дальнейшем для каждого атома
ванадия мы
представляем результаты в локальной системе координат. В ней ось z
направляем на один из наиболее удаленных атомов кислорода (вершинный
кислород) в октаэдре. Направление цепочки атомов ванадия вдоль c
является биссектрисой угла, образуемого осями x и y локальной
системы координат
(рис. 5.3). Эйлеровы углы для перехода из
кристаллографической
системы координат в локальную систему координат для атома ванадия в позиции
(0;0;0) представляют собой набор
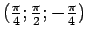 .
.
Таб. 5.1:
Расстояния V-O (ангстремы) для R, M1 и
M2 фаз
VO2.
Наименования кислородов ``вершинный'' и ``плоскостной'' рассматриваются в
локальных системах координат: ось z проходит через вершинный, а оси
x и
y - через плоскостные атомы кислорода.
| атомы кислорода |
R |
M1 |
M2 |
| в димеризованных цепочках |
в недимеризованных цепочках |
| вершинные |
1.93 |
1.76, 2.05 |
1.87 |
1.73, 2.13 |
| плоскостные |
1.92 |
1.86, 1.87, 2.01, 2.03 |
1.85, 2.09 |
1.93, 1.98 |
Поясним термины, которые будут использованы в интерпретации результатов.
Соответствие между t2g
орбиталями в локальных и кристаллографической
системах координат приведено в таблице 4.1.
Под заселенностью i-той орбитали понимается интеграл
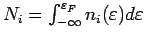 , где
, где
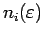 - соответствующая парциальная
плотность состояний, а
- соответствующая парциальная
плотность состояний, а
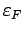 - энергия Ферми. Под центром
тяжести i-той зоны понимается отношение
- энергия Ферми. Под центром
тяжести i-той зоны понимается отношение
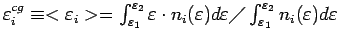 ,
,
где
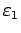 и
и
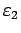 - границы рассматриваемого энергетического интервала.
Под дисперсией i-той зоны понимается выражение
- границы рассматриваемого энергетического интервала.
Под дисперсией i-той зоны понимается выражение
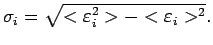 Вследствие искажения
кислородного
октаэдра, t2g орбитали
атома ванадия становятся невырожденными.
Естественным базисом для
t2g орбиталей будут
xy, (yz-zx) и
(yz+zx) волновые функции, где x, y и
z - базис локальной системы
координат. Изображенные орбитали представляют собой угловое распределение
d электронной плотности атомов ванадия
Вследствие искажения
кислородного
октаэдра, t2g орбитали
атома ванадия становятся невырожденными.
Естественным базисом для
t2g орбиталей будут
xy, (yz-zx) и
(yz+zx) волновые функции, где x, y и
z - базис локальной системы
координат. Изображенные орбитали представляют собой угловое распределение
d электронной плотности атомов ванадия
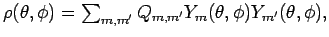 где
где
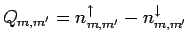 - разность матриц
заселенностей d состояний атомов ванадия со спинами вверх и вниз,
полученных в самосогласованном расчете, а
- разность матриц
заселенностей d состояний атомов ванадия со спинами вверх и вниз,
полученных в самосогласованном расчете, а
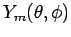 -
соответствующие сферические гармоники (более подробно об этом см. в
разделе 4.2).
-
соответствующие сферические гармоники (более подробно об этом см. в
разделе 4.2).
Рис. 5.4:
Полная (на формульную единицу) и парциальные (на атом)
плотности состояний для R фазы
VO2 (левый столбец), а также
t2g
орбитальная парциальная плотность состояний для атомов ванадия (правый
столбец), полученные в немагнитном LDA расчете. Уровень Ферми обозначен
вертикальными пунктирными чертами. В правом столбце стрелки обозначают
центры тяжести орбитальных парциальных плотностей состояний в
энергетическом интервале от -8 до +6 эВ.
|
|
Рис. 5.5:
Парциальные (на орбиталь) плотности состояний кислорода
для R фазы VO2,
полученные в немагнитном LDA расчете. Уровень Ферми
обозначен вертикальной пунктирной чертой. Наименование орбиталей приведено
в кристаллографической системе координат.
|
|
Результаты немагнитного LDA расчета, предсказывающие металлическое основное
состояние, представлены на рис. 5.4,
5.5, 5.6. Необходимо обратить
внимание (рис. 5.4), что два
атома ванадия, входящие в элементарную ячейку, эквивалентны. Однако
парциальные плотности t2g
состояний эквивалентны только в том случае,
когда они рассматриваются в собственных и отличных друг от друга локальных
системах координат для каждого атома ванадия. Также интересно заметить, что
в предфермиевской области, отмеченной эллипсом
(рис. 5.5),
парциальные плотности кислородных состояний выглядят примерно одинаково.
Другими словами, вклад в кислородную плотность состояний от орбиталей,
параллельных и перпендикулярных тетрагональной оси c, является сравнимым
по величине. Что касается картины зон, то рис. 5.6
демонстрирует, что несмотря на положение xy зоны ниже, чем зоны
(yz-zx) в некоторых направлениях зоны Бриллюэна, занятой
зоной является
зона (yz-zx) в направлении Г-Z. Зона преимущественно
xy характера
лежит выше уровня Ферми в направлении Z-R-A, а зона преимущественно
(yz+zx) характера лежит выше уровня Ферми в направлении
М-Г. Наши LDA
расчеты показывают, что 1) наиболее заселенной является
(yz-zx) орбиталь
вследствие вытянусти кислородного октаэдра вдоль локальной оси z; 2)
центр тяжести (yz-zx) зоны лежит наиболее глубоко в
энергетическом интервале от -8 до +6 эВ; и 3) дисперсия
(yz-zx) зоны примерно в
полтора раза превышает дисперсию xy и (yz+zx) зон
в энергетическом интервале от -1.5 до +1.8 эВ.
Рис. 5.6:
LDA зоны в окрестности уровня Ферми (EF=0) для
R фазы VO2. 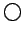 - xy зона;
- xy зона;  - (yz-zx) зона;
- (yz-zx) зона;
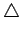 - (yz+zx) зона.
Чем чернее зона - тем более d характер
она имеет (т.е. тем менее вклад кислородных состояний в эту зону): белые
символы - вклад d состояний не меньше 70 %; черные символы -
не меньше 90 %; градация - через 10 %.
- (yz+zx) зона.
Чем чернее зона - тем более d характер
она имеет (т.е. тем менее вклад кислородных состояний в эту зону): белые
символы - вклад d состояний не меньше 70 %; черные символы -
не меньше 90 %; градация - через 10 %.
|
|
Далее были проведены LSDA+U расчеты R фазы
VO2 для ферромагнитного и
антиферромагнитного вдоль цепочек по тетрагональной оси c упорядочения
магнитных моментов ионов ванадия.
Рис. 5.7:
Парциальные плотности состояний атома ванадия,
полученные в LSDA+U расчете ферромагнитного состояния R фазы
VO2.
Уровень Ферми обозначен вертикальной пунктирной чертой. Энергия (абцисса)
- в эВ, плотность состояний (ордината) - в 1/эВ/спин/орбиталь.
Наименование орбиталей приведено в локальной системе координат.
|
|
Рис. 5.8:
LSDA+U зоны в окрестности уровня Ферми (EF=0) для
ферромагнитного состояния R фазы
VO2. 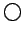 - xy зона;
- xy зона;
 - (yz-zx) зона;
- (yz-zx) зона; 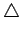 - (yz+zx) зона. Чем чернее
зона - тем более d характер она имеет (т.е. тем менее вклад кислородных
состояний в эту зону): белые символы - вклад d состояний не меньше
60 %; черные символы - не меньше 90 %; градация - через 10 %.
Зоны, сформированные не
t2g состояниями атомов
ванадия, показаны сплошными линиями.
- (yz+zx) зона. Чем чернее
зона - тем более d характер она имеет (т.е. тем менее вклад кислородных
состояний в эту зону): белые символы - вклад d состояний не меньше
60 %; черные символы - не меньше 90 %; градация - через 10 %.
Зоны, сформированные не
t2g состояниями атомов
ванадия, показаны сплошными линиями.
|
|
В первом случае (рис. 5.7, 5.8,
5.9)
получено состояние полуметаллического ферромагнетика со спиновым магнитным
моментом d оболочки ванадия 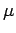 =0.99
=0.99  . Из рис. 5.7 и
5.8 следует, что заполненной становится
(yz-zx) зона и
соответствующая ей орбиталь. Значительные изменения в предфермиевской
области, отмеченной на рис. 5.9 эллипсами, произошли в
парциальной плотности кислородных состояний по сравнению с немагнитным
расчетом. Если LDA результаты предсказывают примерно одинаковый вклад в
кислородную плотность состояний от орбиталей, параллельных и
перпендикулярных тетрагональной оси c, то LSDA+U расчет ферромагнитного
состояния VO2 приводит к
практическому исчезновению плотности
кислородных состояний орбиталей, параллельных оси c. Причиной столь
различного поведения парциальных плотностей кислородных состояний
заключается в гибридизации с
t2g состояниями атомов
ванадия (смотри
рис. 4.5). Как
pX, так и
pY кислородные состояния гибридизованы с
занятыми (yz-zx) ванадиевыми
состояниями, поэтому их плотность состояний в предфермиевскую области
велика. В то же время pZ состояния
гибридизованы только с (yz+zx)
состояниями, которые, согласно расчету, являются незаполненными. Поэтому
плотность состояний pZ орбиталей,
параллельных оси c, в
предфермиевской области пренебрежимо мала.
. Из рис. 5.7 и
5.8 следует, что заполненной становится
(yz-zx) зона и
соответствующая ей орбиталь. Значительные изменения в предфермиевской
области, отмеченной на рис. 5.9 эллипсами, произошли в
парциальной плотности кислородных состояний по сравнению с немагнитным
расчетом. Если LDA результаты предсказывают примерно одинаковый вклад в
кислородную плотность состояний от орбиталей, параллельных и
перпендикулярных тетрагональной оси c, то LSDA+U расчет ферромагнитного
состояния VO2 приводит к
практическому исчезновению плотности
кислородных состояний орбиталей, параллельных оси c. Причиной столь
различного поведения парциальных плотностей кислородных состояний
заключается в гибридизации с
t2g состояниями атомов
ванадия (смотри
рис. 4.5). Как
pX, так и
pY кислородные состояния гибридизованы с
занятыми (yz-zx) ванадиевыми
состояниями, поэтому их плотность состояний в предфермиевскую области
велика. В то же время pZ состояния
гибридизованы только с (yz+zx)
состояниями, которые, согласно расчету, являются незаполненными. Поэтому
плотность состояний pZ орбиталей,
параллельных оси c, в
предфермиевской области пренебрежимо мала.
Рис. 5.9:
Парциальные плотности состояний атома кислорода,
полученные в LSDA+U расчете ферромагнитного состояния R фазы
VO2.
Уровень Ферми обозначен вертикальной пунктирной чертой. Наименование
орбиталей приведено в кристаллографической системе координат.
|
|
Рис. 5.10:
Полная и парциальные (на атом) плотности состояний,
полученные в антиферромагнитном LSDA+U расчете R фазы
VO2.
EF=0.
|
|
Рис. 5.11:
Парциальные плотности V
t2g и O p
состояний,
полученные в антиферромагнитном LSDA+U расчете R фазы
VO2. EF=0.
Наименование орбиталей ванадия приведено в локальной системе координат,
кислорода - в кристаллографической системе координат.
|
|
Во втором случае (рис. 5.10,
5.11)
антиферромагнитное состояние оказалось изолятором с энергетической щелью в
0.38 эВ и 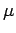 =0.90
=0.90  . Как и в случае ферромагнитного состояния, для
атома ванадия заполненной является (yz-zx) зона и
соответствующая ей
орбиталь, и для атома кислорода плотность состояний
pZ орбиталей,
параллельных оси c, в предфермиевской области пренебрежимо мала (рис.
5.11).
. Как и в случае ферромагнитного состояния, для
атома ванадия заполненной является (yz-zx) зона и
соответствующая ей
орбиталь, и для атома кислорода плотность состояний
pZ орбиталей,
параллельных оси c, в предфермиевской области пренебрежимо мала (рис.
5.11).
Антиферромагнитное решение оказалось ниже ферромагнитного по полной
энергии. Для обоих решений единственный d электрон иона
V4+
локализовался на (yz-zx) орбитали
(рис. 5.12). Это естественным
образом следует из 1) и 2) результатов LDA расчетов: в LSDA+U подходе
заселилась та орбиталь, которая уже и была наиболее заселена, и центр
тяжести которой уже был наинизшим среди всех
t2g орбиталей. Третий же
результат - наибольшая дисперсность (yz-zx) зоны - сохранил
ферромагнитное состояние металлическим даже в LSDA+U расчете и привел к
возникновению антиферромагнитного изоляторного состояния с малой величиной
энергетической щели![[*]](footnote.gif) .
.
Тот факт, что LSDA+U расчеты предсказывают антиферромагнитное изоляторное
состояние для R фазы VO2
вместо немагнитного металлического, отражает
известную тенденцию LSDA+U метода переоценивать электронную локализацию
вследствие рассмотрения спин- и орбитально-зависящего кулоновского
отталкивания на узле в рамках теории среднего поля. В то же время LSDA+U
подход дает аккуратное описание орбитального характера локализованных
электронов![[*]](footnote.gif) .
.
Рис. 5.12:
Упорядочение занятых (yz-zx) орбиталей в цепочке атомов
ванадия, полученное в LSDA+U расчете R фазы
VO2. Обозначения
аналогичные рис. 5.3.
|
|
Наши расчеты электронной структуры
VO2 в R фазе
предсказывают
локализацию d электрона иона
V4+ на
(yz-zx) орбитали. Как будет
видно из последующего, данный результат является ключевым для описания
перехода металл - изолятор в VO2.
Кроме того, исходя из данного результата
общепринятая схема [230] взаимного расположения
t2g
зон ванадия в R фазе VO2
должна быть модифицирована так, как
предложено на рис. 5.13. Еще одним результатом
исследования
особенностей парциальной плотности кислородных состояний является
предсказание существенно различных вкладов в предфермиевской области
от состояний, параллельных и перпендикулярных тетрагональной оси c.
Рис. 5.13:
Схемы взаимного расположения
t2g зон ванадия в
R
фазе VO2: слева -
предложенная Гудинафом в [230];
справа - в настоящем исследовании. Обозначение 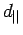 соответствует xy
зоне, параллельной тетрагональной оси c;
соответствует xy
зоне, параллельной тетрагональной оси c; 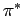 - (yz-zx) и
(yz+zx) зонам, гибридизующимся
- (yz-zx) и
(yz+zx) зонам, гибридизующимся 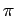 связью с pX,
pY кислородными
состояниями.
связью с pX,
pY кислородными
состояниями.
|
|
Анализ парциальных плотностей
t2g состояний ванадия,
полученных в
немагнитном LDA расчете фазы M1 и
представленных на рис. 5.14,
свидетельствует об иной последовательности заполнения орбиталей по
сравнению с R фазой.
Рис. 5.14:
Полная (на формульную единицу) и парциальные (на атом)
плотности состояний для M1 фазы
VO2 (левый столбец), а также
t2g
орбитальная парциальная плотность состояний для атомов ванадия (правый
столбец), полученные в немагнитном LDA расчете. Уровень Ферми обозначен
вертикальными пунктирными чертами.
|
|
Фаза M1 (пространственная группа
P21/c)
характеризуется спариванием атомов ванадия вдоль вектора
[0.842; 0; -0.539]
в кристаллографической системе координат: имеются короткие и
длинные связи ванадий-ванадий. Кроме того, каждая пара атомов ванадия
наклонена по отношению к этому вектору в плоскости с нормалью
[0.381; 0.708; 0.595]
для одной цепочки атомов ванадия и нормалью
[0.381; -0.708; 0.595]
для соседней цепочки. Отличие кислородного окружения атомов ванадия
заключается не только в изменении углов O-V-O, но и в том, что расстояние
V-O до одного из вершинных атомов кислорода в фазе
M1 стало меньше, чем
в R фазе (таб. 5.1). Локальную
систему координат для фазы M1 мы определяем
следующим образом: ось z
перпендикулярна плоскости атомов ванадия, принадлежащих одной цепочке, а
оси x и y отклонены на 45o от
направления цепочки (рис. 5.15). Другими словами,
локальная система координат для фазы M1
выбирается подобной локальной системе координат для R фазы. Тогда углы
Эйлера для перехода из кристаллографической системы координат в локальную
систему координат для атома ванадия в позиции
(0.259; -0.025; -0.136)
будут 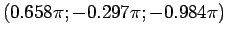 ,
а для атома ванадия в позиции
(0.259; -0.475; -0.731) будут
,
а для атома ванадия в позиции
(0.259; -0.475; -0.731) будут
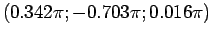 .
.
Рис. 5.15:
Упорядочение занятых xy орбиталей в цепочке атомов
ванадия, полученное в LSDA+U расчетах M1 фазы
VO2. Оси
кристаллографической системы координат обозначены большими буквами,
локальной системы координат для атомов ванадия - малыми.
|
|
Сравнивая парциальные плотности
t2g состояний ванадия
для R и M1
фаз (рис. 5.4 и 5.14), можно
отметить существенную разницу в плотности состояний для xy орбитали.
Для фазы M1 соответствующая зона расщеплена
на связывающую и антисвязывающую
подполосы вследствие димеризации атомов ванадия. И, что наиболее важно,
заполнение xy орбитали становится наибольшим среди
t2g орбиталей.
Немагнитный расчет в приближении LDA не воспроизводит изоляторного
характера энергетического спектра M1 фазы
VO2. Тем не менее ясно, что
учет корреляций в расчетной схеме не изменит этого ключевого результата -
преимущественного заполнения орбитали xy симметрии.
Вывод о заполнении 3d1
xy состояний в фазе M1 поддерживается
двумя
факторами. Во-первых, искажение кислородного октаэдра вокруг атома ванадия
таково, что он становится сжатым вдоль оси z в локальной системе
координат (таб. 5.1), что, в свою
очередь, понижает энергию xy орбитали. И во-вторых, мы провели LSDA+U
расчеты для структуры M1 для того, чтобы
определить, какая из орбиталей
будет заселяться локализованным электроном![[*]](footnote.gif) . Отметим, что LSDA+U
расчет предсказывает антиферромагнитное основное состояние фазы
M1 с
энергетической щелью 0.55 эВ и спиновым магнитным моментом
d оболочки
ванадия
. Отметим, что LSDA+U
расчет предсказывает антиферромагнитное основное состояние фазы
M1 с
энергетической щелью 0.55 эВ и спиновым магнитным моментом
d оболочки
ванадия 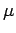 =0.81
=0.81  вместо экспериментально наблюдаемого
немагнитного изолятора сo щелью 0.2-0.7 эВ [251, 237].
По-видимому, квантовые поправки могли бы подавить дальний магнитный
порядок, полученный в LSDA+U расчете, а величина рассчитанной
энергетической щели находится в пределах экспериментальной. Тем не менее,
если вернуться к обсуждению орбитального характера локализованного d
электрона, то, как видно из рис. 5.15, локализованной
орбиталью
стала орбиталь xy. Оба рассмотренных фактора приводят к заключению,
что
при переходе VO2 из R в
M1 фазу вместе с изменением отношения
расстояний от ванадия до кислорода в плоскости и кислорода в вершине
октаэдра происходит важное изменение орбитальной симметрии локализованного
3d1 электрона иона
V4+: от (yz-zx) к xy.
вместо экспериментально наблюдаемого
немагнитного изолятора сo щелью 0.2-0.7 эВ [251, 237].
По-видимому, квантовые поправки могли бы подавить дальний магнитный
порядок, полученный в LSDA+U расчете, а величина рассчитанной
энергетической щели находится в пределах экспериментальной. Тем не менее,
если вернуться к обсуждению орбитального характера локализованного d
электрона, то, как видно из рис. 5.15, локализованной
орбиталью
стала орбиталь xy. Оба рассмотренных фактора приводят к заключению,
что
при переходе VO2 из R в
M1 фазу вместе с изменением отношения
расстояний от ванадия до кислорода в плоскости и кислорода в вершине
октаэдра происходит важное изменение орбитальной симметрии локализованного
3d1 электрона иона
V4+: от (yz-zx) к xy.
По нашему мнению, не механизм Пайерлса ответственен за возникновение
изоляторного состояния фазы M1. Уже LDA
результаты показывают, что
наиболее заполненные орбитали в обоих случаях разные: xy орбиталь для
M1 и (yz-zx) орбиталь для
R фазы. В главе 4 показано,
что (yz-zx) зона является существенно дисперсной и
достаточно сильно гибридизованной с O2p состояниями, образуя с ними 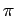 связь. Поэтому
она слабо локализуется даже в присутствии сильных корреляций, и в случае
преимущественного заполнения этой зоны энергетический спектр может остаться
металлическим. В то же время xy зона уже, чем
(yz-zx), и более
чувствительна к корреляциям. Это приводит к локализации электрона на xy
орбитали, ее полному заполнению и открытию щели в энергетическом спектре.
Именно это и случается в наших LSDA+U расчетах. На данном основании можно
сделать вывод о том, что механизм возникновения энергетической щели в
VO2 - мотт - хаббардовский.
Пайерлсовский механизм может быть применен
для объяснения лишь изоляторного состояния фазы
M1, но оказывается
полностью непригодным для фазы M2, в которой
имеются одновременно как
димеризованные, так и недимеризованные цепочки атомов ванадия. С учетом
того, какие орбитали заполняются d электроном в каждом конкретном случае
и каковы свойства этих орбиталей, мотт - хаббардовский механизм оказывается
применимым для описания как металлического, так и изоляторного состояний
всех кристаллических фаз VO2.
связь. Поэтому
она слабо локализуется даже в присутствии сильных корреляций, и в случае
преимущественного заполнения этой зоны энергетический спектр может остаться
металлическим. В то же время xy зона уже, чем
(yz-zx), и более
чувствительна к корреляциям. Это приводит к локализации электрона на xy
орбитали, ее полному заполнению и открытию щели в энергетическом спектре.
Именно это и случается в наших LSDA+U расчетах. На данном основании можно
сделать вывод о том, что механизм возникновения энергетической щели в
VO2 - мотт - хаббардовский.
Пайерлсовский механизм может быть применен
для объяснения лишь изоляторного состояния фазы
M1, но оказывается
полностью непригодным для фазы M2, в которой
имеются одновременно как
димеризованные, так и недимеризованные цепочки атомов ванадия. С учетом
того, какие орбитали заполняются d электроном в каждом конкретном случае
и каковы свойства этих орбиталей, мотт - хаббардовский механизм оказывается
применимым для описания как металлического, так и изоляторного состояний
всех кристаллических фаз VO2.
Расчет электронной структуры фазы
M2
(пространственная группа C2/m)
полностью подтверждает наше предположение о механизме формирования зон в
VO2. В кристаллической структуре
фазы M2 имеются как
димеризованные
цепочки атомов ванадия (аналогичные цепочкам в фазе
M1), так и
недимеризованные (как в R фазе). Углы Эйлера для перехода в локальную
систему координат представляют собой наборы
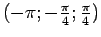 и
и
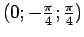 для атомов ванадия в
димеризованных и недимеризованных цепочках (рис. 5.17).
для атомов ванадия в
димеризованных и недимеризованных цепочках (рис. 5.17).
Немагнитные расчеты в приближении LDA дают металлическое основное состояние
в противоречии с экспериментом (рис. 5.16).
Рис. 5.16:
Полная (на формульную единицу) и парциальные (на атом)
плотности состояний для
M2 фазы
VO2, полученные в немагнитном
LDA расчете (левый столбец), а также
t2g орбитальная
парциальная плотность
состояний для атомов ванадия V1, принадлежащих димеризованным цепочкам, и
атомов ванадия V2 из недимеризованных цепочек (правый столбец). Уровень
Ферми обозначен вертикальными пунктирными чертами. Необходимо иметь в виду,
что вследствие низкой симметрии
M2 фазы xy,
yz и zx состояния
выделены из d состояний весьма условно.
|
|
Вследствие существенного искажения кристаллической структуры и,
соответственно, смешивания d состояний ванадия друг с другом, здесь уже
невозможно математически строгим образом выделить парциальные плотности
t2g состояний в
кубических гармониках, как это было нами проделано,
скажем, для R фазы. Однако даже рис. 5.16,
на котором
парциальные плотности состояний атомов ванадия построены с пренебрежением
вкладов, недиагональных между d гармониками, свидетельствует о
заполнении
преимущественно xy орбиталей ванадия в обоих типах цепочек.
Единственной
строгой возможностью определить, какая локализованная
t2g орбиталь
будет заполненной, является LSDA+U расчет.
Рис. 5.17:
Упорядочение занятых xy орбиталей в димеризованной
(левая верхняя часть рисунка) и недимеризованной (нижняя правая часть)
цепочках атомов ванадия, полученное в LSDA+U расчете
M2 фазы
VO2. Оси
кристаллографической системы координат обозначены большими буквами,
локальных систем координат - малыми.
|
|
Результаты такого расчета, представленные на рис. 5.17,
демонстрируют, что в фазе
M2 занятыми орбиталями
ванадия являются xy
орбитали как в димеризованной, так и в недимеризованной цепочках. Было
вычислено, что в случае антиферромагнитного упорядочения величина спинового
магнитного момента d оболочки ванадия, принадлежащего недимеризованной
цепочке, 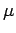 =0.89
=0.89  , а возникающая энергетическая щель имеет
величину 0.93 эВ. Мы также рассчитали обменно-корреляционный параметр
J
модели Гейзенберга между атомами ванадия в недимеризованной цепочке (способ
расчета в рамках LSDA+U метода описан в разделе
6.2). Его величина оказалась равна 205 K,
а знак
соответствует антиферромагнитному обмену. Полученное значение достаточно
близко к данным работы [236], где из анализа результатов
экспериментов по ядерному магнитному резонансу показывается, что ионы
V4+ в недимеризованных цепочках
ведут себя как гейзенберговские
цепочки со спином S=1/2 и антиферромагнитным обменом
, а возникающая энергетическая щель имеет
величину 0.93 эВ. Мы также рассчитали обменно-корреляционный параметр
J
модели Гейзенберга между атомами ванадия в недимеризованной цепочке (способ
расчета в рамках LSDA+U метода описан в разделе
6.2). Его величина оказалась равна 205 K,
а знак
соответствует антиферромагнитному обмену. Полученное значение достаточно
близко к данным работы [236], где из анализа результатов
экспериментов по ядерному магнитному резонансу показывается, что ионы
V4+ в недимеризованных цепочках
ведут себя как гейзенберговские
цепочки со спином S=1/2 и антиферромагнитным обменом
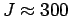 K.
K.
Наше исследование электронной структуры и орбитального заполнения в
VO2
приводит к выводу, что принципиальная разница между фазой рутила R и
моноклинными фазами M1 и
M2 заключается в том,
какая локализованная
t2g орбиталь заполняется
единственным 3d электроном иона
V4+:
(yz-zx) или xy. Выбор заполненной орбитали
определяется локальным
кислородным окружением атомов ванадия. В R фазе заполненной орбиталью
является орбиталь (yz-zx), которая образует 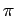 связь с p орбиталями
вершинного кислорода (рис. 4.5).
При переходе VO2 в
M1 и
M2 фазы расстояние
между
атомом ванадия и одним из вершинных кислородов в
M1 фазе и в
недимеризованной цепочке
M2 фазы, или же
между атомом ванадия и обоими
вершинными кислородами в димеризованной цепочке
M2 фазы существенно
уменьшается по сравнению с соответствующим расстоянием в R фазе
(см. таб. 5.1). Это уменьшение расстояния
ведет к усилению p-d гибридизации и, как следствие,
к выталкиванию вверх
выше уровня Ферми (или, что то же самое, к опустошению)
(yz-zx) состояний
атомов ванадия. Именно поэтому при переходе
VO2 из R в
M1 и
M2
фазы происходит смена заполненных зон. Эффект димеризации ванадиевых
цепочек лишь усиливает заполнение xy зоны. Поскольку рассматриваемые
зоны
обладают различными свойствами по отношению к локализации (или дисперсии),
то корреляционные эффекты по-разному сказываются на характере
энергетического спектра (металл или изолятор) в зависимости от того, какая
зона заполнена. Именно корреляции (механизм Мотта-Хаббарда) ответственны за
изоляторные свойства M1
и M2 фаз
VO2.
Корреляции присутствуют и в
металлической R фазе, не приводя к открытию энергетической щели в зонном
спектре вследствие локализации d электрона на
(yz-zx) орбитали.
связь с p орбиталями
вершинного кислорода (рис. 4.5).
При переходе VO2 в
M1 и
M2 фазы расстояние
между
атомом ванадия и одним из вершинных кислородов в
M1 фазе и в
недимеризованной цепочке
M2 фазы, или же
между атомом ванадия и обоими
вершинными кислородами в димеризованной цепочке
M2 фазы существенно
уменьшается по сравнению с соответствующим расстоянием в R фазе
(см. таб. 5.1). Это уменьшение расстояния
ведет к усилению p-d гибридизации и, как следствие,
к выталкиванию вверх
выше уровня Ферми (или, что то же самое, к опустошению)
(yz-zx) состояний
атомов ванадия. Именно поэтому при переходе
VO2 из R в
M1 и
M2
фазы происходит смена заполненных зон. Эффект димеризации ванадиевых
цепочек лишь усиливает заполнение xy зоны. Поскольку рассматриваемые
зоны
обладают различными свойствами по отношению к локализации (или дисперсии),
то корреляционные эффекты по-разному сказываются на характере
энергетического спектра (металл или изолятор) в зависимости от того, какая
зона заполнена. Именно корреляции (механизм Мотта-Хаббарда) ответственны за
изоляторные свойства M1
и M2 фаз
VO2.
Корреляции присутствуют и в
металлической R фазе, не приводя к открытию энергетической щели в зонном
спектре вследствие локализации d электрона на
(yz-zx) орбитали.
Наши выводы могли бы быть подвергнуты экспериментальной проверке. Для этого
необходимо произвести измерения зонной структуры валентной полосы
VO2
как в изоляторной, так и в металлической фазе, а также поверхности Ферми
для металлической фазы. Например, исследование предфермиевской области
кислородной плотности состояний в металлической фазе может напрямую
свидетельствовать о важности корреляций, если сигнал вдоль и поперек
тетрагональной оси c будет существенно разным, как предсказывается в
настоящей работе. Современное экспериментальное оборудование и методики
позволяют проводить подобные исследования на синхротронах, например с
использованием фотоэлектронной спектроскопии с угловым разрешением.
Существует проект проведения таких исследований на синхротроне в г.
Гренобле (Франция), который планируется в группе проф. Чьенга из
Университета г. Кельна (Германия). В качестве аргументации необходимости
проведения исследования VO2
им были использованы результаты, описанные выше.
Результаты исследования электронной структуры и перехода металл - изолятор в
диоксиде ванадия VO2 были
доложены автором на рабочем совещании
``Корреляционные эффекты в расчетах электронной структуры'' (Ляйден,
Нидерланды, ноябрь 2001 г.), на ежегодном собрании голландских физиков в
г. Эйндховен (Нидерланды, декабрь 2001 г.), на коллоквиуме во втором
Физическом институте Университета г. Кельна (Германия,
декабрь 2001 г.), а
также опубликованы в журнале ``Физика металлов и металловедение'' [19].
Сноски:
- ... фаз
![[*]](footnote.gif)
- Существуют экспериментальные
оценки величины кулоновского взаимодействия U в
VO2 [237] -
2.1 эВ для изоляторной фазы и 1.3 эВ для металлической фазы.
Эти значения
несколько меньше используемого в расчетах U=3.8 эВ.
- ... щели
![[*]](footnote.gif)
- При величине
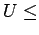 3.0 эВ и
антиферромагнитное состояние R фазы в LSDA+U расчете является
металлическим. Смотри также предыдущую сноску.
3.0 эВ и
антиферромагнитное состояние R фазы в LSDA+U расчете является
металлическим. Смотри также предыдущую сноску.
- ...
электронов
![[*]](footnote.gif)
- Это показано в серии наших работ по исследованию
орбитального заполнения в CrO2
[15], перовскитах
PrMnO3
[14],
La7/8Sr1/8MnO3
[18], слоистых ванадатах типа
CaVnO2n+1
[16, 17] и др.
- ... электроном
![[*]](footnote.gif)
- При расчете M1 и
M2 фаз
VO2 основывать выводы
на сравнении центров тяжестей орбиталей
и дисперсий соответствующих зон, полученных в немагнитных LDA расчетах,
становится некорректным вследствие низкой симметрии этих фаз и
значительного смешивания исследуемых состояний.
Следующая страница: Глава 6.
``Магнитные свойства Ca(Mg)VnO2n+1''
Предыдущая страница: Глава 4.
``CrO2 - самолегированный
ферромагнетик с механизмом двойного обмена''
Вернуться к содержанию диссертации
![]() 0.1 ат.%) [232] или при небольшом
напряжении вдоль оси
0.1 ат.%) [232] или при небольшом
напряжении вдоль оси 


![]() кластерного метода
дискретного варьирования привело к появлению щели в зонном спектре [247]. Введение поправки на самодействие
в рамках модельной GW
схемы также удовлетворительно воспроизвело экспериментальные свойства
неметаллической
кластерного метода
дискретного варьирования привело к появлению щели в зонном спектре [247]. Введение поправки на самодействие
в рамках модельной GW
схемы также удовлетворительно воспроизвело экспериментальные свойства
неметаллической ![[*]](footnote.gif) . Таким образом,
проведенные расчеты не содержат подгоночных параметров и в этом смысле
являются первопринципными.
. Таким образом,
проведенные расчеты не содержат подгоночных параметров и в этом смысле
являются первопринципными.

![]() .
.
![]() , где
, где
![]() - соответствующая парциальная
плотность состояний, а
- соответствующая парциальная
плотность состояний, а
![]() - энергия Ферми. Под центром
тяжести i-той зоны понимается отношение
- энергия Ферми. Под центром
тяжести i-той зоны понимается отношение
![]() ,
, ![]() и
и
![]() - границы рассматриваемого энергетического интервала.
Под дисперсией i-той зоны понимается выражение
- границы рассматриваемого энергетического интервала.
Под дисперсией i-той зоны понимается выражение
![]() Вследствие искажения
кислородного
октаэдра,
Вследствие искажения
кислородного
октаэдра, ![]() где
где
![]() - разность матриц
заселенностей d состояний атомов ванадия со спинами вверх и вниз,
полученных в самосогласованном расчете, а
- разность матриц
заселенностей d состояний атомов ванадия со спинами вверх и вниз,
полученных в самосогласованном расчете, а
![]() -
соответствующие сферические гармоники (более подробно об этом см. в
разделе 4.2).
-
соответствующие сферические гармоники (более подробно об этом см. в
разделе 4.2).





![]() =0.99
=0.99 ![]() . Из рис. 5.7 и
5.8 следует, что заполненной становится
. Из рис. 5.7 и
5.8 следует, что заполненной становится



![]() =0.90
=0.90 ![]() . Как и в случае ферромагнитного состояния, для
атома ванадия заполненной является
. Как и в случае ферромагнитного состояния, для
атома ванадия заполненной является ![[*]](footnote.gif) .
.
![[*]](footnote.gif) .
.



![]() ,
а для атома ванадия в позиции
,
а для атома ванадия в позиции
![]() .
.

![[*]](footnote.gif) . Отметим, что
. Отметим, что ![]() =0.81
=0.81 ![]() вместо экспериментально наблюдаемого
немагнитного изолятора сo щелью 0.2-0.7 эВ [251, 237].
По-видимому, квантовые поправки могли бы подавить дальний магнитный
порядок, полученный в
вместо экспериментально наблюдаемого
немагнитного изолятора сo щелью 0.2-0.7 эВ [251, 237].
По-видимому, квантовые поправки могли бы подавить дальний магнитный
порядок, полученный в ![]() связь. Поэтому
она слабо локализуется даже в присутствии сильных корреляций, и в случае
преимущественного заполнения этой зоны энергетический спектр может остаться
металлическим. В то же время xy зона уже, чем
связь. Поэтому
она слабо локализуется даже в присутствии сильных корреляций, и в случае
преимущественного заполнения этой зоны энергетический спектр может остаться
металлическим. В то же время xy зона уже, чем
![]() и
и
![]() для атомов ванадия в
димеризованных и недимеризованных цепочках (рис. 5.17).
для атомов ванадия в
димеризованных и недимеризованных цепочках (рис. 5.17).


![]() =0.89
=0.89 ![]() , а возникающая энергетическая щель имеет
величину 0.93 эВ. Мы также рассчитали обменно-корреляционный параметр
J
модели Гейзенберга между атомами ванадия в недимеризованной цепочке (способ
расчета в рамках
, а возникающая энергетическая щель имеет
величину 0.93 эВ. Мы также рассчитали обменно-корреляционный параметр
J
модели Гейзенберга между атомами ванадия в недимеризованной цепочке (способ
расчета в рамках ![]() K.
K.
![]() связь с p орбиталями
вершинного кислорода (рис. 4.5).
При переходе
связь с p орбиталями
вершинного кислорода (рис. 4.5).
При переходе ![[*]](footnote.gif)
![[*]](footnote.gif)
![[*]](footnote.gif)
![[*]](footnote.gif)